Путенихин П.В.

О сущности ускоренного расширения Вселенной

On the essence of the accelerated expansion of the Universe

 

Аннотация

Что означает ускоренное или замедленное расширение Вселенной? Приведено определение понятия космологического ускорения и уравнение для его вычисления.

What does the accelerated or slowed down expansion of the universe mean? The definition of the concept of cosmological acceleration and the equation for its calculation are given.

 

Ключевые слова: космологическое ускорение, параметр замедления, параметр Хаббла, масштабный фактор, ускоренное расширение Вселенной, красное смещение

 

О сущности ускоренного расширения Вселенной

 

В наших рассуждениях мы постоянно использовали понятие ускоренного, равномерного или замедленного расширения Вселенной. Однако чёткого определения этих понятий, что мы под ними подразумеваем, мы пока не привели. Более того, представления о механизмах, лежащих в их основе, весьма неопределённые и у многих других исследователей. Вследствие этого возникают довольно спорные выводы по проявлениям этих механизмов. В частности, существует мнение, что ускоренное расширение Вселенной напрямую связано с уменьшением параметра Хаббла во времени. Если параметр Хаббла уменьшается, то это означает ускоренное расширение Вселенной. Сторонники этого подхода приводят, например, аргумент, уравнение, который, по их мнению, определённо подтверждает такое мнение:

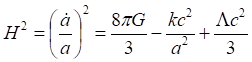(1)

Утверждается, что вид этой формулы лишает всякой возможности придумать убывающую функцию масштабного фактора a(t), при которой убывал бы и параметр Хаббла. Действительно, из этого уравнения, на первый взгляд, явно следует, что росту масштабного фактора соответствует убывание параметра Хаббла. Однако перепишем уравнение условно и кратко:

Теперь уже точно видно: при росте масштабного фактора a параметр Хаббла H может только возрастать! Это происходит из-за знака минус перед членом, содержащим масштабный фактор, в результате чего при его росте вычитается всё меньшая и меньшая величина, а результат, соответственно, возрастает.

Заметим, что и само понятие "ускоренное расширение Вселенной" имеет некоторую двусмысленность. Все объекты в расширяющейся Вселенной по определению движутся с ускорением. В самом деле, масштабный фактор Вселенной, пространство которой расширяется равномерно, описывается уравнением:

Это уравнение и собственно масштабный фактор и его производная по времени относятся ко всей Вселенной в целом, описывает каждую точку его пространства. В наблюдательной астрономии у них есть физические эквиваленты: конкретные дистанции между объектами (например, в световых годах) и скорости убегания (например, в долях от скорости света). Эти эквиваленты, соответственно, относятся только к этим двум объектам. В дальнейшем мы не будем акцентировать внимание на отмеченных особенностях, а просто будем подразумевать их тождество. В приведённой записи имеется в виду некоторый нулевой момент времени, когда масштабный фактор был ненулевым, равным некоторому начальному значению a₀. Соответственно, эти два эквивалентных подхода имеют и эквивалентные уравнения:

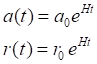
Обе величины – масштабный фактор и дистанция можно связать единичным коэффициентом:

Смысл коэффициента – это длина, например, стандартного метра r₀ в пространстве с масштабным фактором a₀. Дифференцированием находим и такую же связь между скоростями изменения этих величин, представляющую закон Хаббла:

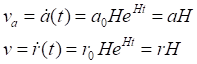(2)

C учётом коэффициента находим выражение, которое выглядит, по сути, как простая замена переменных:

(3)

Хотя обычно мы оперируем масштабными факторами, это же уравнение, как видим, можно записывать и с реальными физическими переменными – скоростью и удалённостью.

Существует общепризнанная гипотеза, что обнаруженное ускоренное расширение Вселенной вызвано действием тёмной энергии. Но все объекты удаляются друг от друга с ускорением и в равномерно расширяющейся Вселенной. Из (3) мы явно видим, что скорость убегания объекта непрерывно возрастает. Это видно и из уравнений (2). Двойное дифференцирование показывает, что объекты не только удаляются с некоторым ускорением, но и само ускорение непрерывно растёт:

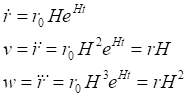
Уравнение для ускорения весьма похоже на стандартный закон Хаббла. Сразу же замечаем некоторые странности в трактовке таких ускорений. Понятно, что любой удаляющийся во Вселенной объект обладает некоторой массой. Следовательно, для его ускоренного движения необходимо приложить к нему какую-то силу, затратить некоторую энергию:

Странность состоит в том, что для наблюдателей слева этот объект ускоренно убегает вправо, а для наблюдателя справа – влево. Если инициатором убегания является некая сила, энергия, пусть даже и загадочная тёмная, то вопросы остаются одними и теми же: в какую сторону эта сила, энергия толкает удаляющийся объект? Сколько сил или тёмных энергий толкают объект, если с разных точек зрения он движется с разным ускорением?

Неясным оказался и вопрос о связи переменного параметра Хаббла и характером расширения Вселенной: ускоренным или замедленным. Хотя ответ видится достаточно очевидным, но по нему нередко возникают довольно жаркие дискуссии. Например, в одной такой дискуссии бы предложен весьма красивый и поучительный пример. Предложено уравнение масштабного фактора, явно стремительно возрастающего во времени:

Видим, что это уравнение описывает параболу с ветвями, направленными вверх. С ростом времени до бесконечности, так же до бесконечности возрастает и масштабный фактор. Автор этого примера задаёт весьма коварный вопрос: описывает ли это уравнение Вселенную, расширяющуюся ускоренно?

Вроде бы ответ очевиден. Правда, он опирается на неявное определение понятия ускоренного расширения. Понятно, что уравнение точно соответствует расширяющейся Вселенной, но ускоренной ли? Далее следует ещё один, решающий вопрос: чему при этом равен параметр Хаббла? Догадываемся, что отвечающий должен прийти к противоречию, получив для якобы для ускоренно расширяющейся Вселенной убывающий параметр Хаббла. В самом деле, находим его:

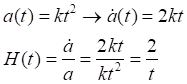
И, действительно, мы получили параметр Хаббла, явно убывающий во времени. При этом произведший его масштабный фактор растёт. Что же получилось? Масштабный фактор растёт, а параметр Хаббла убывает, то есть, ускоренно расширяющейся Вселенной соответствует убывающий масштабный фактор. Но здесь мы вновь укажем на неправомерное отождествление "расширяющаяся" Вселенная и "ускоренно расширяющаяся" Вселенная.

Поэтому на вопросы автора рассмотренного примера был дан ответ: это расширяющаяся Вселенная, и притягивать её к хаббловской ускоренной неуместно. В классическом представлении закона Хаббла ускорения здесь не видно.

Следует пояснить эти утверждения. Сначала приведём данное в ответе четкое определение понятию "ускоряющаяся Вселенная". Ускоряющейся Вселенной следует считать такую, в которой в каждый последующий момент, интервал времени дистанция между некими двумя объектами увеличилась больше, чем в предыдущий момент, за такой же интервал времени. Скажем, вчера – в два раза, а сегодня – в четыре. Как вариант: за прошлый год некая исходная дистанция между двумя объектами возросла в 2 раза. А за этот год такая же исходная дистанция между другими двумя подобными объектами возросла в 4 раза. Можно сказать, что в этом определении уже достаточно отчётливо заметно решение задачи. Тем не менее, сторонники иного решения предложили собственное:

Хотя детального, подробного описания этого высказывания, представленного как решение, не приведено, можно лишь догадаться, что имелось в виду. Поскольку вторая производная больше нуля, то масштабный фактор определённо возрастает. Пожалуй, это единственное разумная трактовка высказывания, из которой, по всей видимости, должно следовать, что убывающему параметру Хаббла точно соответствует возрастающий масштабный фактор. Но эта единственная трактовка вызывает удивление: эта величина, эта вторая производная, вообще-то, определённо относится к разделу функционального анализа. Если первая производная некоторой функции равна нулю, что это означает наличие экстремума. Вторая производная определяет характер этого экстремума: её положительная величина означает минимум функции ("есть вода"), отрицательная – максимум функции ("нет воды"), а нулевая – точку перегиба. Кстати, знак третьей производной в этой точке описывает характер экстремума: нуль – это "чистый экстремум" – минимум или максимум. Знак указывает направление роста в точке перегиба – от меньших значений к большим и наоборот. Вероятно, автору указанного "решения" пояснили его ошибочность, поэтому в дальнейшем он явным образом отказался от него.

Заметим, что масштабный фактор в рассматриваемом примере при положительности второй производной имеет на самом деле области, как возрастания, так и убывания. То есть, и предложенное ошибочное решение и связка "растущий масштабный фактор" и "убывающий параметр Хаббла" не доказывают, что они соответствуют ускоренно расширяющейся Вселенной.

Но каково же тогда верное решение, которое, как ожидается, доказывает обратное: убывающий параметр Хаббла означает замедленно расширяющуюся Вселенную? В рассмотренной дискуссии было предложено три таких решения, три доказательства.

Первое решение обозначено как краткое, простое, но исчерпывающее и описывается уравнением:

Согласно этому уравнению со временем параметр Хаббла стремится к нулю, из чего сразу же следует соответствующий вид закона Хаббла:

Получается, что в далёком будущем скорость удаления объектов друг от друга стремится к нулю. Но это стационарная Вселенная. Если сегодня она расширяющаяся, неважно, с ускорением или с замедлением, то, в конечном счете, становится стационарной. Очевидно, говорить о дальнейшем ускоренном расширении такой Вселенной нет никакого смысла. Если ранее Вселенная расширялась, неважно как, то теперь она расширяться перестала, а это прямо означает замедленное расширение. Вплоть до прекращения всякого расширения. Следовательно, уменьшение параметра Хаббла привело к замедлению и остановке расширения Вселенной.

Тем не менее, факт остаётся фактом: с указанным масштабным фактором Вселенная расширяется, причём размеры её растут всё больше и больше. Как же такая Вселенная может быть стационарной?

И здесь мы отметим явную подмену понятий. Увеличение масштабного фактора, всех интервалов во Вселенной происходит не как некая абстракция, а как наблюдательный факт. Если бы Хаббл производил свои наблюдения в такой Вселенной на самых поздних строках роста масштабного фактора согласно приведённому уравнению, то он не обнаружил бы никакого разбегания, никакого красного смещения. Это прямо следует из приведённого позднего закона Хаббла.

Причина, источник такого кажущегося противоречия и суть подмены состоят в том, что определение характера расширения Вселенной на самом деле сводится к сравнению дистанций в разные моменты времени, но за один и тот же интервал наблюдений. Скорость удаления объектов, определяющую характер расширения Вселенной находят по их красному смещению:

Уточним, что индекс 0 соответствует настоящему, нашим дням. В рассматриваемой задаче мы можем определить по красному смещению z относительную скорость разбегания двух объектов:

Рассмотрим некоторый определённый интервал времени, скажем, тысячу лет. Тогда

Если мы сравниваем объекты в самом начале расширения Вселенной, скажем, в момент времени 1000 лет от Большого Взрыва, то получаем:

Теперь рассмотрим, как быстро, спустя 10⁹ лет, удаляются друг от друга такие же два объекта, за такой же интервал времени наблюдения – 1000 лет:

То есть, через 10⁹ лет при рассматриваемом законе роста масштабного фактора наблюдатель не обнаружит никакого относительного движения галактик. Для сравнения рассмотрим, что будет в случае стандартного расширения Вселенной с современным значением постоянной Хаббла:

Здесь, напомним, a₀ – это исходное, начальное значения масштабного фактора для двух наблюдаемых объектов. Вблизи начального момента времени за такой же период наблюдений: (t₀ – t₁) = 1000 мы обнаружим

Теперь произведёт такие же измерения, спустя 10⁹ лет. В этом случае, с учётом моменты наблюдений возрастут до: t₀' = t₀+10⁹ и t₀' = t₁+10⁹. Соответственно, за такой же интервал наблюдений – 1000 лет, то есть мы получим значение красного смещения:

Подставляем сюда стандартные, современные законы изменения масштабного фактора

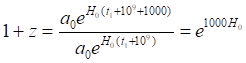
То есть, и в наши дни и спустя 10⁹ лет при неизменном параметре Хаббла H₀ и современном законе изменения масштабного фактора мы получаем одно и то же красное смещение. Очевидно, это соответствует равномерному расширению Вселенной. Таким образом, этот пример также соответствует предложенному определению ускоренного, равномерного или замедленного расширения Вселенной, определяемому по характеру изменения параметра Хаббла.

Последний вариант доказательства использует более явное и наглядное изменение параметра Хаббла.

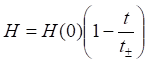
в данном случае параметр H(0) – это не нынешнее его значение H₀, а некоторое положительное исходное значение, значение в начальный момент расширения Вселенной.

Из уравнения мы видим, что в некоторый момент времени t_± параметр Хаббла становится равным нулю, то есть, Вселенная перестаёт расширяться, становится стационарной. Далее параметр становится отрицательным, а Вселенная начинает сжиматься, причём на бесконечности – до нулевых размеров. Закон Хаббла с таким характером уменьшения параметра Хаббла можно записать в следующем виде

Это означает, что при изменении параметра Хаббла от некоторой положительной до некоторой отрицательной величины расширение Вселенной заменяется на её сжатие.

Используемое понятие "космологическое ускорение" не имеет соответствующего мнемонического обозначения, как некая физическая величина. Во всяком случае, широко распространённого и общепризнанного в литературе мы не встретили. Поскольку понятие явно означает ускорение, введём для удобства такое обозначение в виде ускорения w_H:

Теперь мы можем дать формальное определение:

 

Определение космологического ускорения:

Космологическим ускорением расширяющейся или стационарной Вселенной w_H является первая производная по времени параметра Хаббла.

Величина космологического ускорения имеет размерность [t^–2] – обратная величина квадрата времени. Приведём возможные варианты расширения Вселенной в зависимости от характера изменения параметра Хаббла:

– параметр Хаббла возрастает во времени, w_H > 0 – это ускоренно расширяющаяся Вселенная; считается, что в наши дни Вселенная расширяется именно так: ускоренно;

– параметр Хаббла неизменный во времени, w_H = 0, но не равный нулю – это равномерно расширяющаяся Вселенная;

– параметр Хаббла неизменный во времени, w_H = 0, и равен нулю – это стационарная Вселенная;

– параметр Хаббла убывает во времени, w_H < 0, но имеет положительное значение – это замедленно расширяющаяся Вселенная; такими были представления о расширении Вселенной до открытия её ускоренного расширения, и появления гипотезы о тёмной энергии;

– параметр Хаббла убывает во времени, w_H < 0, и имеет отрицательное значение – это сжимающаяся вплоть до сингулярности Вселенная.

Выведем уравнение для вычисления параметра космологического ускорения w_H из уравнений масштабного фактора. Используем классическое определение параметра Хаббла:

(4)

Дифференцированием находим параметр "космологическое ускорение" как величину, имеющую конкретное количественное, численное значение:

(5)

Это же уравнение можно вывести и другим путём:

Выделяем из него первую производную:

Дифференцированием находим вторую производную:

Преобразуем для выделения первой производной параметра Хаббла:

Подставляем значение параметра Хаббла из (4):

Наконец, разделяем переменные и выделяем величину космологического ускорения:

(5.8.20)

Таким выходящим из общего ряда номером уравнения мы обозначили день его рождения. Уравнение появилось в воображении автора ранним утром 5 августа 2020 года. Отметим, что за некоторое подобие этого параметра можно принять так называемый параметр замедления:

Физический смысл этого параметра довольно туманный, не очень понятно, что же именно он обозначает. Его смысл определённо следует признать хуже физического смысла введённого нами космологического ускорения w_H.

В качестве примера определим параметр космологического ускорения w_H для Вселенной, расширяющейся с неизменным значением параметра Хаббла. Запишем совместно, одним блоком уравнения масштабного фактора и его производных:

Подставляем в уравнение (5):

Как видим, значение ускорения равно нулю, что и означает равномерное расширение Вселенной, без ускорения. Теперь приведём пример масштабного фактора с некоторым условным параметром Хаббла, соответствующим ускоренно расширяющейся Вселенной:

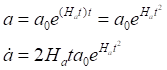
Здесь величина H_at является неким усреднённым, интегральным параметром Хаббла. Сам параметр определяем из (4):

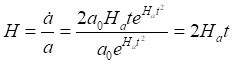
Для определения параметра космологического ускорения, как и выше, запишем компактно уравнения масштабного фактора и его производных:

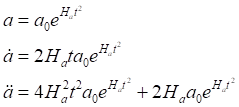
Теперь определяем для этой ускоренно расширяющейся Вселенной значение параметра космологического ускорения w_H, подставив найденные величины в (5):

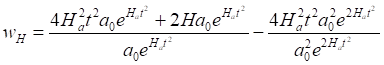
Сокращаем дроби и находим:

Этот параметр можно было вычислить и напрямую из выражения для найденного параметра Хаббла:

В заключение найдём величину космологического ускорения, этот же параметр w_H и для проблемного примера, считавшегося примером ускоренного расширения Вселенной. Пример на самом деле описывает замедленное расширение Вселенной:

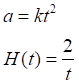
Дифференцированием по времени находим:

Видим, что параметр ускорения отрицательной, что и означает замедленное ускорение расширяющейся Вселенной. Было бы интересно определить параметр космологического ускорения для уравнения (1),

но в нём не указан закон изменения масштабного фактора, поэтому мы можем получить только визуальный вывод о замедленном расширении Вселенной с последующим переходом в состояние равномерного расширения:

Мы нашли, что параметр Хаббла – положительная ненулевая величина, а его производная по времени – отрицательна. Согласно нашей классификации это уравнение соответствует космологическому замедлению, замедленному расширению Вселенной.

Рассмотренное уравнение относится к формализму современной космологии, придерживающейся модели с тёмной энергией. Было бы правильным дать оценку космологического ускорения в этой модели. Для этого, очевидно, нам необходимы либо уравнения движения, либо диаграммы. К сожалению, почти во всей в литературе по этой теме в точной количественной форме уравнения движения отсутствуют, а диаграммы представлены в весьма завуалированном виде. Выявить на них численное значение космологического ускорения, задача довольно нетривиальная.

Вместе с тем, косвенно такую оценку параметру космологического ускорения можно дать, например, по рисунку в статье [1]:

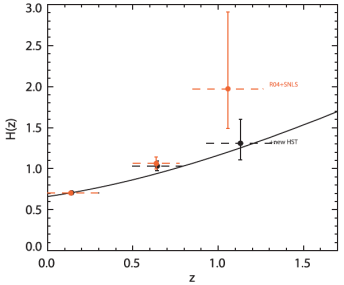
"... положительный или отрицательный знак наклона данных указывает на замедление или ускорение расширения соответственно". Рисунок из статьи [1]

 

Что на рисунке следует считать положительным или отрицательным знаком наклона? Сделаем очевидные выводы. На рисунке представлен график зависимости нормированного параметра Хаббла от красного смещения H(z) по наблюдениям за сверхновыми. Сразу же отмечаем, параметр Хаббла для сверхновых с красным смещением 1,5 больше, чем для сверхновых c красным смещением, близким к нулю ~ 0,15. Принято считать, что информация о параметрах сверхновых тем более старая, чем выше их красное смещение. Буквально это означает, что красное смещение 1,5 соответствует прошлому, то есть, более раннему времени существования сверхновой. Из этого мы делаем вывод, что раньше значение параметра Хаббла было больше, чем в наши дни. Количественно в представленных координатах мы можем вычислить соответствующе среднее эквивалентное космологическое ускорение w_z:

Поясним причину появления знака минус. В знаменателе мы имеем интервал "времени", за который произошло изменение параметра Хаббла. По определению это разница всегда положительна. В числителе мы записали разницу между новым нормированным значением параметра Хаббла, практически в наши дни (0,65) и тем, что было в прошлом (1,7). В результате мы имеем право сделать вывод: значение параметра Хаббла (нормированное) больше нуля, а скорость его возрастания, ускорение – отрицательно. Согласно нашей модели это означает замедленное расширение Вселенной.

Примерно к такому же выводу пришёл и Решетников, правда, с несколько компромиссной формулировкой:

"Видно также, что открытие ускоренного расширения не означает, что уже сейчас темп расширения Вселенной растет. На самом деле он еще падает, но не так быстро, как ранее ожидалось – замедление расширения Вселенной тормозится и когда-нибудь постоянная Хаббла, действительно, начнет расти" [2].

То есть, сегодня Вселенная расширяется всё-таки замедленно, вопреки гипотезе о тёмной энергии. Но она будет когда-то расширяться ускоренно. Вместе с тем в исходной, цитированной статье вывод явно прямо противоположный:

"... мы измерили H(z) ... усилив доказательства космического рывка – перехода от замедления в прошлом к ускорению в настоящем"

"Эти полдюжины SN Ia ... помогли подтвердить реальность космического ускорения, очерчивая переход от предшествующего космического замедления во время фазы, в которой преобладает материя..." [1].

Тем не менее, указанное "подтверждение" определённо противоречит представленному графику, на котором логически непротиворечиво просматривается иное: Вселенная в наши дни расширяется замедленно.

 

Литература

 

1. Riess, A.G. et al. 2007, ApJ, 659, 98. New Hubble Space telescope discoveries of type Ia supernovae at z ≥ 1: narrowing constraints on the early behavior of dark energy, URL: https://iopscience.iop.org/article/10.1086/510378/pdf

2. Решетников В.П., Почему небо темное. Как устроена Вселенная. Издательство "Век-2", 2012, URL: www.astro.spbu.ru/staff/resh/Books/acceluniv.pdf

 

 

---

Сконвертировано и опубликовано на https://SamoLit.com/