Vector properties of the gravitational potential
Векторные свойства гравитационного потенциала
Путенихин П.В.
Аннотация
Приведено доказательство векторной природы гравитационного потенциала, согласно которой гравитационный потенциал в любой точке бесконечной Вселенной равен нулю. Напротив, согласно скалярным представлениям о гравитационном потенциале, в стационарной Вселенной гравитационный потенциал равен бесконечности, причём в любой точке пространства. Однако этот потенциал входит в уравнение всемирного тяготения, имеющего явно векторный характер. Закон неявно содержит в себе не только ускорение свободного падения, векторную величину, но и формирующий его гравитационный потенциал, который автоматически получает статус вектора.
The proof of the vector nature of the gravitational potential is given, according to which the gravitational potential at any point of the infinite Universe is equal to zero. On the contrary, according to scalar concepts of gravitational potential, in a stationary Universe, the gravitational potential is equal to infinity at any point in space. However, this potential is included in the equation of universal gravitation, which is clearly vector in nature. The law implicitly contains not only the acceleration of gravity, a vector quantity, but also the gravitational potential that forms it, which automatically receives the status of a vector.
Ключевые слова: стационарная Вселенная, закон всемирного тяготения, сфера Хаббла, ускорение свободного падения, гравитационный парадокс, вектор, деление на вектор, вектор близости
Гравитационный потенциал
Гравитационные взаимодействия характеризуются двумя основными понятиями – силой гравитационного притяжения и гравитационным потенциалом. Хотя очевидно, что сила гравитационного притяжения является вектором, уравнение закона всемирного тяготения, тем не менее, записывают в виде скаляра. В связи с этим отметим одно интересное наше наблюдение. Если какая-то величина может иметь отрицательное значение, то такую величину определённо можно считать вектором. В частности, закон всемирного тяготения иногда пишут со знаком минус
![]()
При этом нередко уточняется, что знак минус означает притяжение. Логически это легко объяснимо. Если масса находится в начале координат, то все положительные векторы направлены "наружу", от этого начала. Но сила притяжения направлена извне в сторону тела, в сторону начала координат. То есть, её можно рассматривать как отрицательный скаляр, так и как вектор, направленный в сторону начала координат. Но если эта величина, сила является вектором по указанной выше минусовой причине, записать это можно в следующей векторной форме
![]()
Знак минуса отбрасываем, поскольку направление силы теперь определяется вектором. Поскольку в записи под знаком вектора имеются константы, их можно вынести
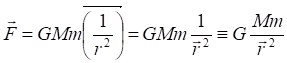
Запись, как видим, приобрела более явный векторный вид. Однако в знаменателе присутствует квадрат вектора или, по меньшей мере, произведение вектора на самого себя
![]()
Известны два произведения векторов: векторное и скалярное. В нашем случае скалярное произведение неприменимо, поскольку его результат – скаляр, то есть, уравнение перестаёт быть векторным. Но и векторное произведение нас не устраивает, поскольку в этом случае направление вектора уже не совпадает с направлением силы. Выход только один: один из одинаковых сомножителей в знаменателе должен потерять статус вектора
![]()
На первый взгляд, это ничем не обоснованный произвол в записи уравнения. В сущности, величиной вектора мы можем считать и квадрат скаляра. Но пока рассмотрим другой вариант, ведущий к интересным выводам. Перепишем уравнение ещё раз с учетом разделения сомножителей
![]() (1)
(1)
Замечаем, что левый сомножитель в последнем равенстве выглядит как традиционный гравитационный потенциал тела M, но записанный в векторной форме. Насколько это оправдано? Почему не обозначить вектором второй, правый сомножитель, а первый оставить в прежней, не векторной форме? Конечно, это возможно и до данного момента используется повсеместно, но в этом случае векторная форма второго сомножителя приобретает весьма неясную форму. А вот векторная форма гравитационного потенциала приобретает весьма осмысленный вид с далеко идущими последствиями.
Действительно, сила притяжения двух тел пропорциональна модулю такого векторного гравитационного потенциала и направлена строго по соединяющей два тела линии. Иначе говоря, налицо признаки вектора: величина (длина) и направление. Более того, если поменять местами массы, то получим
![]() (2)
(2)
теперь уже это уравнение гравитационного потенциала малого тела. Очевидно, что направление вектора, его знак в этом случае меняются на противоположные. То есть, вновь мы получаем достаточно осмысленное соотношение. Кстати, можно заметить, что запись для гравитационного потенциала в несколько ином виде была бы более наглядна:
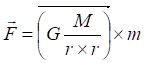 (3)
(3)
Запись гравитационного потенциала, левого сомножителя в форме вектора придало бы уравнению более определённый смысл. А именно: величина силы в точке нахождения малого, так называемого пробного тела равна произведению его массы на значение потенциала. Но эта форма записи уже "занята" – это ускорение свободного падения. Если сократить уравнения на эту малую, внешнюю массу, получим соотношение
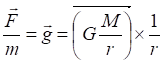 (4)
(4)
Теперь можно заметить, почему мы не использовали в качестве вектора обратную величину квадрата расстояния. Бесспорно, что вектором в выражении (3) может быть только величина в скобках, левый сомножитель, поскольку масса определённо величина не векторная. Это выражение является одной из записей закона Ньютона – сила равна произведению массы на ускорение. То есть, в этом выражении (3) векторная величина в скобках является ускорением. В нашем случае это вполне определённое ускорение – ускорение свободного падения на тело (планету) массой M.
Если сократить выражение (3) на массу m, то получим инверсную запись закона Ньютона (4). Как видим, ускорение свободного падения не зависит от массы падающего тела. В этом выражении (4) мы также можем вынести за векторные скобки скалярные величины.
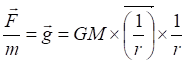 (5)
(5)
Два правых крайних сомножителя тождественны до векторного "звания". Здесь у нас нет никакого выбора, какой из них вектор – вектором может быть только один из этих двух тождественных величин. Вместе с тем, отметим, что средний сомножитель (6) сам по себе имеет довольно туманный векторный смысл
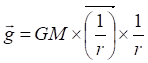 (6)
(6)
Введём новый термин – близость по аналогии с терминами электротехники – сопротивление и проводимость, являющимися взаимно обратными величинами. Соответственно, в законе гравитации такими взаимно обратными величинами можно считать удалённость и близость.
Следует признать, что вектор близости или, тождественно, обратной величины удалённости в уравнении (6) сам по себе имеет весьма туманный, неопределённый смысл. Однако, в уравнении имеется "свободный", скалярный сомножитель, левый. Конечно, куда его поместить, как говорится, дело вкуса. Однако, замечаем некоторое сходство уравнения (6) и уравнения (3). Если в уравнении (3) мы вынесем за векторные скобки одну из тождественных величин – близостей, что определённо является разумным, и сократим на массу m, то получим тот же результат, что и при внесении в векторные скобки уравнения (6) этой скалярной величины GM
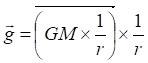 (7)
(7)
Получается, что выше в выражении (4) вектором мы справедливо признали величину, содержащую это массивное тело, поскольку вывели мы его из выражения (3), в котором векторной величиной в скобках однозначно и очевидно является величина, также содержащая эту массу – ускорение свободного падения g. Таким образом, вполне логично и даже бесспорно признать, что величина (7), ускорение свободного падения является вектором – у неё есть и величина и направление. Следует признать, что мы доказываем, причём весьма скрупулёзно, по сути, довольно очевидное обстоятельство: ускорение свободного падания является вектором. Однако это обстоятельство имеет большое значение: гравитационный потенциал можно трактовать через это ускорение. А именно: величина ускорения свободного падения в данной точке равна произведению гравитационного потенциала притягивающего тела в этой точке на её близость к этому телу. Близость, напомним, это обратная величина удалённости, то есть
![]() (8)
(8)
Следовательно, это выражение (8), как и (1) также бесспорно является верным – векторами в них являются левые сомножители. Таким образом, мы считаем доказанным и строго обоснованным утверждение, что гравитационный потенциал является векторной величиной. В связи с этим отметим ещё одно очень важное следствие из векторной формы гравитационного потенциала:
![]()
Интегрирование этого векторного уравнения даже по всему бесконечному пространству Вселенной даёт нулевое значение. Иначе говоря: гравитационный потенциал от всего вещества Вселенной в каждой точке пространства равен нулю точно так же, как и от конечной сферически симметричной области окружающего пространства. В сущности это очевидно и без вычислений, без интегрирования. Для заданной точки в бесконечной стационарной изотропной Вселенной для любой удалённой точки всегда найдётся другая точка, симметричная ей и создающая такой же по величине, но противоположный по направлению вектор гравитационного потенциала, сводящий суммарный потенциал к нулю. В таком виде гравитационный парадокс, как видим, теряет свой первоначальный смысл.
Отметим небольшую условность в наших формах записи вектора гравитационного потенциала. Поскольку операция деления скаляра на вектор не определена, правильнее векторное уравнение потенциала записывать без указания удалённости (близости) как самостоятельно вектора, а рассматривая его как скалярную величину в составе собственно вектора потенциала
![]()
Хаббловский гравитационный потенциал
Наши выкладки сделаны для стационарной Вселенной. В расширяющейся Вселенной на гравитационный потенциал точки влияет масса только видимой части Вселенной, то есть, галактики и другие объекты, находящиеся в пределах сферы Хаббла. Всё, что дальше границы сферы, никакого гравитационного влияния на центр сферы Хаббла не оказывают, поскольку скорость их удаления превышает скорость света и, соответственно, скорость распространения гравитационного притяжения.
Очевидно, что речь может идти только об условном гравитационном потенциале в точке на сфере Хаббла, формируемым всем веществом внутри этой сферы. Расчёт этой величины, видимо, не представляет особого труда, поскольку известны и средняя плотность вещества Вселенной и радиус сферы Хаббла. Хотя реального, механического удаления галактик нет, видимо, всё-таки следует учитывать и релятивистские эффекты – рост массы объектов, удаляющихся с субсветовыми скоростями, что несколько усложняет расчёты.
Адрес статьи в интернете:
http://samlib.ru/editors/p/putenihin_p_w/grav_pot180.shtml
12.12.2020 – 07.02.2021
Сконвертировано и опубликовано на https://SamoLit.com/


