В.А.Сыромясский.

ПРОБЛЕМЫ МЕХАНИКИ

Часть 1

Запорожье

2003

УДК 531

ББК В2

С953

Сыромясский В.А.

C953 Проблемы механики. – Запорожье

ISBN 966 – 599 – 133 - 7

В этой книге вниманию читателя предложен критический анализ формулировок основных законов механики и традиционных воззрений на природу соударений твердых тел, принятых в теоретической и прикладной механике. Показана противоречивость ряда определений и понятий, несоответствие их действительной физике явлений. Предложена динамическая модель соударений, новая измерительная техника и методика исследований. На этой основе сформулированы уточнения и изменения к ряду законов, аксиом и определений. Дано определение понятию удар как многофакторному физическому процессу. Приведены примеры практического использования предложенных теоретических положений при создании новых образцов техники эксперимента и эффективно работающего оборудования в различных отраслях промышленного производства. Показана природа вибрационного транспортирования сыпучих материалов.

Книга может быть полезна научным работникам, конструкторам, исследователям, а также желающим углубить свои знания в области теоретической и практической механики.

УДК531

ББК В2

ISBN 966-599-133-7 © Сыромясский В.А., 2003

© Лешкевич И.И., 2003

© Тарасов И.В., 2003

Предисловие

В настоящей публикации ставится несколько необычная задача рассмотрения ряда противоречий в толковании основных законов механики и связанных с этим проблем в объяснении природы динамического контактного взаимодействия твердых упругих тел. Тех противоречий и разночтений законов, которые накопились за довольно значительный период развития теоретической механики и которые своим рождением обязаны усилиям ревнителей непреложности однажды установленных истин и незыблемости авторитета их канонизированных отцов-основателей. А также усилиями тех, кто пожелал присовокупить к общему достоянию своё видение добрых старых истин и свои новации. В результате, как это нам представляется, теоретическая механика на страницах научных и учебных изданий стала постепенно терять очертания строгой научной дисциплины и превращаться в эклектический сборник суждений, сомнений и разночтений. Особенно это находит проявление в толковании основных воззрений механики на такие вещи, как масса твердого тела, инерция, сила, ускорение, динамическое контактное взаимодействие (удар). Ради справедливости следует заметить, что начало этому положили сами великие. В подтверждение приведём некоторые их высказывания.

И. Ньютон: «Выражение для силы – есть всего лишь правила, согласующиеся с кинематическими опытами».

Д. Аламбер: «Силы – туманные понятия».

Пуанкаре: «Когда говорят, что сила есть причина движения,– то это метафизика».

Д. Мэрион в книге «Физика и физический мир»:
«Логическая структура динамики таит в себе сложности, обойти которые, по-видимому, невозможно. Никому ещё не удавалось найти неопровержимый переход к динамике – на пути всегда возникает дилемма силы и массы».

Особый интерес представляют высказывания учёных-представителей прикладных наук, близко стоящих к реализации крупных научно-технических проблем.

Профессор Калифорнийского Технологического института Р.Фейнман (31):
«Все физические законы отличаются своим абстрактным характером. Закон сохранения энергии – это теорема о величинах, которые нужно вычислить и сложить, не думая о причине этого; точно так же и великие законы механики представляют собой количественные математические закономерности, о внутреннем механизме работы которых данных нет. Почему мы можем пользоваться математикой для описанных законов, не зная их причины? Никто этого не знает. Мы продолжаем идти по этой дороге, потому что на ней всё ещё происходят открытия».
«Одна из важнейших характеристик силы – её материальное происхождение; и это свойство как раз нельзя считать определением. Ньютон привел ещё одно правило, касающееся сил: силы между взаимодействующими телами равны и противоположны; действие равно противодействию. И это правило, оказывается не совсем верно. Да и сам закон F = ma не совсем верен; будь он определением, мы должны были бы утверждать, что он точно верен всегда, а на самом деле это не так. Любое простое высказывание является приближенным. Сколько бы вы не настаивали на точном определении силы, вы его никогда не получите».

Авторы совремённой версии прикладной теории ударных систем Е.В.Александров и В.Б.Соколинский (9):
«Методы теории упругости дают более правильный и точный результат, чем классической механики, и тем не менее на практике пользуются «классическим вариантом» ввиду сложности понимания и громоздкости расчетов по первому направлению. Однако такое положение нетерпимо, ибо очень часто встречаются задачи, для которых решения классической механики дают совершенно неправильные результаты».

До настоящего времени как со стороны классической механики, так и со стороны теории упругости, не нашел окончательного решения механизм динамического контактного взаимодействия твердых тел, не снят с вооружения ньютоновский несколько уже одиозный «принцип дальнодействия».

Р.Файнман (31) об упругом столкновении двух тел равных масс: «Если такие тела ударяются друг о друга с какой-то скоростью, то по соображениям симметрии они должны разлететься в стороны с той же скоростью».

Как видим, всё очень просто. Только остаётся неизвестным, знают ли о нашем «соображении» упомянутые тела.

Можно было бы привести ещё один очень характерный пример того, как изящно обходит препятствия высокая наука. Л.Д.Ландау и Е.М.Лившиц в пособии для физиков-теоретиков «Механика»: «Тот факт, что потенциальная энергия зависит только от расположения точек в один и тот же момент времени, означает, что изменение положения одной из них мгновенно отражается на всех остальных; можно сказать, что взаимодействия «распространяются» мгновенно. Неизбежность такого характера взаимодействий в классической механике тесно связано с основными предпосылками последней – абсолютностью времени и принципом относительности Галилея».

При изложении и толковании основных законов классической механики часто возникают дискуссии о том, какой из них считать действительно фундаментальным законом природы, а какой можно квалифицировать как следствие первого. Многочислены также попытки дать собственноё видение и изложение того, что только недавно воспринималось как истина в последней инстанции.

Возьмём, к примеру, первый закон Ньютона, который в изначальной редакции звучит так (2): «Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».

Дж. Б.Мэрион (21): «Если действующая на тело результирующая сила равна нулю, то ускорение тела равно нулю и тело движется с постоянной скоростью».

А.А.Яблонский (17): «Материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не изменит это состояние».

И.Е.Иродов (15): «Утверждение, что инерциальные системы отсчёта существуют, составляет содержание первого закона классической механики – закона инерции Галилея-Ньютона».

C.П.Стрелков (18): «В этом законе, называемом первым законом Ньютона, прежде всего, имеется утверждение, что покой и равномерное и прямолинейное движение тела – одно и то же механическое состояние тела».

Л.Д.Ландау, Е.М.Лившиц (5): «В инерциальной системе отсчета всякое свободное движение происходит с постоянной по величине и направлению скоростью. Это утверждение составляет содержание так называемого закона инерции».

Оставим в стороне стилистический произвол авторов и постоянную подмену ими предмета обсуждения. Но остаётся несомненным, что истинный закон природы не может определяться столь разноречиво. Чем глубже он познан и верно осознан, тем меньше он оставляет свободы для разночтений. Закон – это философская категория, отражающая существенное, общее, необходимое, устойчивое, повторяющееся для данной области отношение между явлениями объективной реальности. Законы внутренне присущи предметам и явлениям и выступают в качестве принципа их организации и функционирования. Они не могут быть «так называемыми» и приспособляемыми по необходимости.

Суммируя всё изложенное ранее, мы выражаем солидарность с Е.В.Александровым в том, что «такое положение нетерпимо».

Известно, что при формулировке основных законов механики Ньютоном были сделаны допущения, позволившие перебросить мост между приложением силового воздействия и получением конечных результатов, игнорируя физическую суть процессов, происходящих в промежутке (периоде) между этими двумя событиями. Основным из этих допущений является, как уже отмечалось ранее, принцип дальнодействия. Следует отметить, что упрощённую схему взаимодействия тел первым принял Х.Гюйгенс в своём трактате «О движении тел под влиянием удара» (7). Свою гипотезу под номером два он изложил так: «Не входя в рассмотрение причины отскакивания твёрдых тел после соударения, принимаем следующее положение: если два одинаковых тела, движущихся с одинаковой скоростью навстречу друг другу, сталкиваются прямым ударом, то каждое из них отскакивает назад с той же скоростью, с какой ударилось».

Теперь, вооружившись накопленными знаниями и совершенными средствами измерения, мы должны ещё раз пройти этот путь от начала до конца, не обходя никаких препятствий. Основной задачей на этом пути будет построение непрерывной цепи механических эволюций, которые испытывают реальные физические тела в процессе их динамического контактного взаимодействия во времени и пространстве. Для того чтобы избежать в процессе этой работы возможных ошибок и предубеждений, полезно было бы провести предварительно своего рода инвентаризацию основных положений классической механики и на её основе сформулировать возможные вопросы и спланировать необходимые эксперименты. Что мы и проделаем в последующих разделах.

Глава 1
Классическая механика.
Вопросы и сомнения

Рассмотрим наиболее часто встречающиеся формулировки законов, теорем, допущений и определений, которые используются в научных, учебных и справочных источниках. На основе их анализа и сопоставления попытаемся выявить существующие противоречия или недостаточно корректные выводы и на этой основе сформулировать вопросы и задачи по проведению необходимых исследований и экспериментов.

1.1Закон всемирного тяготения.

Тяготение существует ко всем телам вообще пропорционально массе каждого из них.

Сила гравитационного притяжения, действующая между двумя материальными точками, пропорциональна произведению масс точек, обратно пропорциональна квадрату расстояния между ними и направлена по прямой, соединяющей эти точки.

У Ньютона (2) это изложено так:

«
Притяжение каждого шара другим обратно пропорционально квадрату расстояния между центрами их :

где γ – гравитационная постоянная;
m₁ и m₂ – массы взаимодействующих точек;
r – расстояние между ними».

Ясно, что для случая с «материальными точками» формула виртуальна. Возникает вопрос, может ли величина r принимать значения меньше единицы, или существуют какие-то другие ограничения? Влияет ли на величину гравитационной силы конфигурация взаимодействующих тел?

Закон всемирного тяготения И.Е.Иродов (15) сопровождает следующим комментарием: «Фигурирующие в этом законе массы называют гравитационными в отличие от инертной массы, входящей во второй закон Ньютона. Из опыта, однако, установлено, что гравитационная и инертная массы любого тела строго пропорциональны друг другу. Поэтому можно считать их равными, то есть выбрать один и тот же эталон для измерения масс и говорить просто о массе, которая выступает как мера инертности тел или как мера гравитационного действия».

Здесь остаются не ясными такие вопросы:

Так равны или всё-таки пропорциональны массы друг другу?

Что означает здесь слово «строго»?

Могут ли принадлежать одному и тому же телу две разные массы?

1.2Первый закон механики Ньютона.

В оригинале (Собрание трудов А.Н.Крылова, т.7, изд. АН СССР, 1936, М. Стр.39) закон изложен Ньютоном как аксиома:

«Всякое тело продолжает удерживаться в своём состоянии покоя или равномерного и прямолинейного движения, пока и поскольку оно не понуждается приложенными силами изменить это состояние».

Христиан Гюйгенс в своём труде «Три мемуара по механике» (М.,1951) излагает этот закон как гипотезу:

«Тело, приведенное в движение, при отсутствии противодействия продолжает своё движение неизменно с той же скоростью и по прямой линии».

А.А.Яблонский в учебнике «Курс теоретической механики» (Высшая школа, М., 1966, стр. 8) излагает этот же закон как утверждение:

«Материальная точка сохраняет состояние покоя или равномерного прямолинейного движения, пока воздействие других тел не изменит это состояние».

Имея ввиду, что гипотетическая «материальная точка» в последней формулировке физически не может воздействовать на реальное тело, будем считать, термин «материальная точка» адекватным понятию «всякое тело». Принимая во внимание приведенное ранее понятие категории закона, будем полагать, что физическое тело, которому посвящен этот закон, это обособленный и самодостаточный предмет природы, к уже известным свойствам которого (массе, цвету, конфигурации и т. п.) мы намерены дать определение последнего: его способности к движению. Эта способность, естественно, должна измеряться определенными параметрами. В связи с этим возникает вопрос, почему авторы рассматриваемого закона используют такие определения, как «продолжает удерживаться», «продолжает своё движение» или «сохраняет состояние покоя или движения»? Ни в обиходе, ни в научной практике мы не говорим о том, что какое-то тело сохраняет приданную ему окраску, конфигурацию или, скажем, вес. Термины «сохраняют», «удерживают», «продолжают» логически подразумевают наличие некоторой причины, противодействующей чему-то. А из «практики нам известно, что свободному движению тела абсолютно ничего не препятствует.

Что касается формулировок, предложенных для первого закона механики Мэрионом, Иродовым, Стрелковым и рядом других авторов, то в них прослеживается подмена субъекта, о котором идет речь – физического тела, на такие понятия, как «результирующая сила», «инерциальные системы отсчета», «покой и равномерное движение». Узнать о них подробнее конечно интересно, но это совершенно другая тема.

Приведенные примеры иллюстрируют несколько свободный подход к трактовке первого закона механики. Особенно это относится к последующему разъяснению приведенных формулировок, к которому прибегают авторы в разных вариациях. Например, в упомянутой книге С.П.Стрелкова «Механика» имеется такое пояснение: «В этом законе, называемом первым законом Ньютона, прежде всего имеется утверждение, что покой и равномерное и прямолинейное движение тела – одно и то же механическое состояние тела». Но в дословном переводе формулировок Ньютона этого утверждения нет, отсутствуют также указания о возможных следствиях. В этом плане сентенция о существовании инерциальных систем, может быть, и соответствует истине, но не составляет предмета выводов Ньютона. Вызывает сомнение целесообразность и такой реконструкции формулировки первого закона, предложенной Мэрионом, в которой на первый план поставлена сила, а затем тело, состоянию которого, собственно, и посвящен первый закон. Изложение сути первого закона не выигрывает от произведенной замены понятий прямолинейного и равномерного движения на понятие равного нулю ускорения и постоянной скорости. Утверждение в формулировке А.А.Яблонского о воздействии других тел на материальную точку следует признать не вполне корректным.

В постановке Ньютона исследуется и утверждается способность физического тела «продолжать удерживаться в своём состоянии покоя и прямолинейного движения». Возникает вопрос: почему отдаётся приоритет или исключительность только прямолинейному движению? Не вызывает сомнения, что то же тело с таким же успехом способно сохранять и равномерное вращательное движение. Например, пуля, выпущенная из нарезного ствола, продолжает одновремённо прямолинейное движение переноса и вращательное вокруг собственной оси.

Аргументированное подтверждение этому мы находим в «Механике» Л.Д.Ландау и Е.И.Лифшица:

«
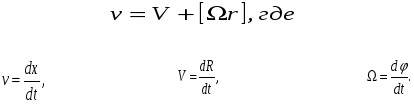
Для твердого тела, совершающего одновремённо движения переноса и вращения относительно собственной оси

И, соответственно,
x – координата центра инерции тела;
R – радиус-вектор;
– угол вращения;
– вектор угловой скорости.

Вектор V есть скорость центра инерции твердого тела; её называют также скоростью его поступательного движения. Вектор называется угловой скоростью вращения твердого тела; его направление (как и направление d) совпадает с направлением оси вращения. Таким образом, скорость v любой точки тела (относительно неподвижной системы координат) может быть выражена через поступательную скорость тела и угловую скорость его вращения».

1.3Второй закон механики Ньютона

В оригинале (Собрание трудов А.Н.Крылова, т.7, 1936, М., стр. 40) изложен как аксиома:

«Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует».

У
Ньютона (2) этот закон выражался соотношением:

В
своём трактате «Механика» Эйлер придал этому выражению другую форму:

Эта форма написания закона стала общепринятой.

И.Е.Иродов (Основные законы механики. 1978.,М., стр.37,40):

«Ускорение материальной точки в инерциальной системе отсчета прямо пропорционально действующей на неё силе и обратно пропорционально её массе:

г

де F – в общем случае есть равнодействующая всех сил, приложенных к данной материальной точке».

Далее к своей формулировке второго закона механики он даёт следующие разъяснения и комментарии.

«Произведение массы материальной точки на её ускорение является функцией положения этой точки относительно окружающих тел, а иногда и функцией её скорости. Эту функцию обозначают F и называют силой.

Произведение массы материальной точки на её ускорение равно действующей на неё силе, то есть mw=F.

С
ила есть производная импульса p материальной точки по времени, то есть

С.П.Стрелков («Механика», 1965, М., стр.65) :

«Производная от количества движения тела равна по величине действующей силе и совпадает с ней по направлению».

.А.А.Яблонский («Курс теоретической механики». 1966, М., стр.8):

«Ускорение материальной точки пропорционально приложенной к ней силе и имеет одинаковое с ней направление».

Д

.Б.Мэрион («Физика и физический мир», 1975, М., стр.139).

«Ускорение движения тела может быть вызвано только силой, приложенной к этому телу. Ускорение пропорционально действующей на тело силе, причём коэффициент пропорциональности характеризует инерцию, или массу тела, то есть, F=ma.»

Р.Фейнман (Фейнмановские лекции по физике. Изд. «Мир», М., 1976, стр.162).

«Количественной мерой инертности является масса. Если масса постоянна, то F = mdvdt = ma.

Второй закон Ньютона означает не только то, что изменения, вызванные данной силой, обратно пропорциональны массе, но и то, что направление изменения скорости совпадает с изменением силы».

Г.К.Суслов («Теоретическая механика», 1946, стр.135).

«Сила характеризуется: 1) точкой приложения; 2) модулем; 3) направлением».

Прежде чем приступить к анализу приведенных формулировок, настоятельно необходимо согласовать систему терминов и понятий, а также последовательность событий физического свойства, опираясь на философский тезис о том, что время есть организация последовательностей.

Ньютон в разделе «Математические начала натуральной философии» законам предпослал следующие определения:

1.Количество материи (масса) есть мера таковой, устанавливаемая пропорционально плотности и объёму.

2.Количество движения есть мера такового, устанавливаемая пропорционально скорости и массе (p=mv).

3.Приложенная сила есть действие, производимое над телом, чтобы изменить его состояние покоя или равномерного прямолинейного движения. Сила проявляется единственно только в действии и по прекращении действия в теле не остаётся. Тело продолжает затем удерживать своё новое состояние вследствии одной только инерции. Происхождение приложенной силы может быть различное: от удара, от давления, от центростремительной силы.

4.Врожденная сила материи есть присущая ей способность сопротивления, по которой всякое отдельно взятое тело, поскольку оно предоставлено самому себе, удерживает своё состояние покоя или равномерного прямолинейного движения.

Итак, построим логическую цепь событий, отражающих второй закон механики.

И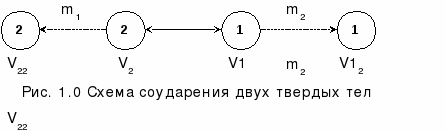
меем тело m₁, движущееся с некоторой скоростью v₁ и обладающее количеством движения p=m₁v₁. Воздействуем на него другим телом m₂, движущимся со скоростью v₂>v₁ и обладающим количеством движения p₂=m₂v₂ по той же линии движения.

В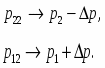
результате воздействия скорость V₂ уменьшится, а V₁ увеличится. соответственно:

С
прашивается, где (в какой точке, сечении или объёме) была гипотетическая «сила» в то время, когда во взаимодействующих телах одно движение порождало другое, и была ли необходимость её присутствия в принципе? Не являлся ли причиной, вызвавшей изменение состояния тела m₁ импульс p₂, материализованный через массу m₂?

О
бозначим «приложенную движущую силу» через F. Тогда, строго следуя тексту второго закона механики, мы должны записать:

С
другой стороны

где k – коэффициент передачи механической энергии движения между взаимодействующими телами.

Современная интерпретация второго закона механики не может не вызывать некоторого недоумения.

Если Ньютон определил предметом рассмотрения физическое тело и количественную характеристику его движения, то И.Е.Иродов рассматривает ускорение материальной точки в инерциальной системе отсчета. А.А.Яблонский предметом второго закона считает ускорение материальной точки безотносительно системы отсчета, а Д.Мэрион говорит об ускоренном движении тела как такового. С.П.Стрелков в отличие от Ньютона считает, что производная от количества движения тела не пропорциональна, а равна по величине действующей силе. Г.К.Суслов утверждает, что сила характеризуется точкой приложения.

Рассмотрим особо одну из формулировок, приведенных И.Е.Иродовым: «произведение массы материальной точки на её ускорение равно действующей на неё силе, то есть mw=F.» Каков физический смысл этой величины? С одной стороны – это математический приём определения величины изменения импульса движения (количества движения), и к категории фундаментальных законов природы не относится. С другой стороны – это физическое состояние тела, характеризующее конец акта передачи механической энергии. Если сила F, предшествующая изменению количества движения, вызвала это изменение в такой же размерности, как и она сама, то налицо механизм с коэффициентом полезного действия равным единице. А это невозможно. Так как сила F – уже состоявшийся факт, то её никуда уже приложить невозможно, ни в точке ни тем более в центре масс или центре инерции. Тогда зачем нам эту силу искать? Не похоже ли это на погоню за призраком? Спрашивать, какая сила подействовала на тело массой m, которое в результате получило скорость V, так же некорректно, как спрашивать, сколько стоит мешок зерна? Здесь неизбежно потребуется уточнение: какой мешок, какого зерна, и что такое стоит?

1.4Третий закон механики Ньютона

В первоисточнике (труды А..Н.Крылова, т.7, изд. АН СССР,1936, М.) изложен как аксиома:

«Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны.»

И.Е.Иродов («Основные законы механики», 1978, М.,стр.43):

«Всякое действие тел друг на друга носит характер взаимодействия. Две материальные точки действуют друг на друга с силами, равными по величине и направленными в противоположные стороны вдоль прямой, соединяющей эти точки, то есть F₁₂= -F₂₁».

А.А.Яблонский («Курс теоретической механики», т.2, 1966, М., стр.8.):

«Всякому действию соответствует равное и противоположно направленное противодействие.»

Д.Б.Мэрион («Физика и физический мир», 1975, М., стр.140):

«Если тело 1 действует на тело2 с какой-либо силой, то тело 2 действует на тело 1 с равной противоположно направленной силой. Таким образом, любая сила всегда встречается в паре с равной по величине противодействующей силой F₁₂= -F₂₁».

Прежде чем перейти к обсуждению физической сущности третьего закона, попытаемся выяснить, что же является его объектом: конкретное тело, бесконечно малая частица или лишенная размеров точка? Можно ли говорить о том, что действия тел друг на друга адекватны независимо от их размеров, масс, протяженности и прочностных характеристик? Допускает ли закон «представительство» материальных точек при рассмотрении реально происходящих физических процессов? Или, напротив, распространяется ли закон на реальные протяженные и объёмные физические тела? И последнее. Как быть с предпосланными Ньютоном данному закону гипотезами об абсолютно твёрдом теле и принципе дальнодействия?

В комментарии И.Е.Иродова (15,стр.41) присутствует следующее разъяснение:

«В третьем законе Ньютона предполагается, что обе силы равны по модулю в любой момент времени независимо от движения точек. Это утверждение соответствует ньютоновскому представлению о мгновенном распространении взаимодействий – предположению, которое носит название принципа дальнодействия классической механики. Согласно этому принципу взаимодействие между телами распространяется в пространстве с бесконечной скоростью».

Г.К.Суслов (16,стр.137) изложение закона сопроводил следующим комментарием:

«Высказанный закон подразумевает, что речь идет о силах, действующих на частицы бесконечно малых размеров. Иначе нельзя было говорить о прямой противоположности действия и противодействия, так как точек приложения сил было бы бесчисленное множество. Когда силы приложены к телам, занимающим конечные объёмы, надо предварительно разбить мысленно эти тела на бесконечно малые элементы и затем уже группировать силы «действия и противодействия».

Приведём ещё одно характерное рассуждение Д.Б.Мэриона (21, стр.141) о применимости третьего закона:

«Третий закон не может применяться в тех случаях, когда для передачи действия силы требуется конечное время. Но передача всех основных сил в природе происходит за конечное время; следовательно, третий закон выполняется совершенно строго только в том случае, когда взаимодействующие тела находятся в состоянии покоя; при этом не происходит изменений сил, и представление о времени передачи воздействия оказывается ненужным».

Отметим, что во всех рассуждениях о взаимодействии реальных тел присутствует интуитивное представление о том, что силы, возникшие на контакте взаимодействующих тел непосредственно ответственны за последующие движения рассматриваемых тела – «отталкиваются друг от друга». Далее мы рассмотрим процесс «отталкивания» более подробно.

Всё это напоминает известную притчу о том, сможет ли всемогущий Бог создать камень, который сам не сможет поднять. Если тело абсолютно твердое, то, при воздействии на него другого тела, его граничный объём не сдвинется ни на йоту, а все последующие сечения «не узнают» вообще, что такое событие было. Если же сообщение о контакте мгновенно распространилось до противоположной границы, то, как это могло произойти, если в силу абсолютной твердости лобовое сечение не сдвинулось ни на йоту?

Так логический дефект в суждении приводит к сомнительным выводам.

1.5Законы сил

1.5.1Сила тяжести.

В разделе 1.1 уже изложены сведения о гравитационной силе, определяемой в соответствии с законом всемирного тяготения. Эта сила господствует над всем материальным миром и очевидно является праматерью любого механического движения.

В условиях Земли на все предметы действует сила тяжести, обусловленная массой Земли. В непосредственной близости к поверхности Земли поле земного притяжения принято считать постоянным и однородным. Однородная сила тяжести

F = mg ,

где m -масса тела;
g -ускорение силы тяжести.

Вес P-это сила, с которой тело действует на опору или подвес, неподвижные относительно данного тела. Если тело с опорой неподвижны относительно Земли, то вес P совпадает с силой тяжести. В противном случае вес

P = m (g-a),

где a - ускорение тела с опорой относительно Земли.

1.5.2Упругая сила.

В общем случае говорят о квазиупругой силе. В этом случае упругая сила определяется как величина, пропорциональная смещению частицы из положения равновесия и направленная к положению равновесия:

F = - kr,

где r-радиус-вектор, характеризующий смещение частицы из положения равновесия;

k- положительный коэффициент, зависящий от упругих свойств той или иной конкретной силы.

Применительно к деформации пружины или стержня эта сила в соответствии с законом Гука определяется как

F = kL,

где L – величина упругой деформации.

Экспериментально установлено, что для большинства твердых тел деформации пропорциональны приложенной нагрузке, если только нагрузка не превосходит некоторого значения, называемого пределом упругости. Математически этот экспериментальный закон формулируется так: каждая из шести компонент напряжения в любой точке тела является линейной функцией шести компонент деформации, то есть

_xx=C_11xxC_12ууC_13zzC_14уzC_15zxC_16xу

_ууC_21xxC_22ууC_23zzC_24уzC_25zxC_26xу

_zzC_31xxC_32ууC_33zzC_34уzC_35zxC_36xу

_уzC_41xxC_42ууС_43яяС_44уzC_45zxC_46xу (1.1)

_zxC_51xxC_52ууС_53zzС_54уzC_55zxC_56xу

_xуC_61xxC_62ууС_63zzС_64уzC_65zxC_66xу

Здесь коэффициенты представляют собой упругие постоянные материала; первая буква в индексе напряжения означает его направление, а вторая – плоскость, на которую оно действует.

Рассмотренная запись формулы носит название обобщенной формы закона Гука.

Условие того, что упругая энергия является однозначной функции деформации, состоит в равенстве коэффициентов C_rs и C_sr. При этом число независимых коэффициентов уменьшается от 36 до 21. В изотропном теле значения коэффициентов не должно зависеть от выбора прямоугольной системы осей, откуда вытекает, что независимых постоянных здесь только две. Обозначим их и .. Тогда C₁₂=C₁₃=C₂₁=C₂₃=C₃₁=C₃₂=

C₄₄=C₅₅=C₆₆=

C₁₁=C₂₂=C₃₃= + 2,

а остальные двадцать четыре коэффициента равны нулю. Уравнения (1.1) принимают вид:

_xx2_xx,

_уу2_уу,

_zz2_zz, (1.2)

_уzуz,:

_zxzx,

_xуxу,

где _xxууzz выражает изменение объёма единичного куба и называется дилатацией или объёмным расширением.

Две упругие постоянные и называются константами Ляме и полностью определяют упругие свойства тела. Для удобства обычно используют четыре упругие постоянные: модуль продольной упругости , пуассоново отношение , модуль объёмного сжатия и модуль сдвига, cвпадающий с константой . С помощью уравнений (1.1) , и можно выразить через и .

Модуль можно определить как отношение напряжения к относительному удлинению, когда к цилиндрическому образцу приложено равномерно распределённое по плоским концевым сечениям напряжение, а боковая поверхность свободна. Если ось x параллельна оси цилиндра, то _xx – приложенное напряжение, а другие компоненты напряжения равны нулю. Первые три уравнения при этом дают

_xx2_xxууzz,

2_ууzzxx,

2_zzxxуу.

Р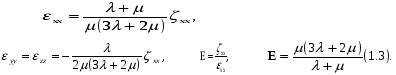
азрешив эти уравнения относительно _xx, _уу, и _zz, получим

Пуассоново отношение определено как отношение поперечного сокращения к продольному удлинению образца при свободной боковой поверхности, то есть в рассматриваемом случае как - _ууxx.

О
тсюда

Модуль объёмного сжатия определяется как отношение приложенного давления к относительному изменению объёма тела, подверженного равномерному гидростатическому сжатию. При этих условиях _xx=_уу=_zz=-P и _уz=_zx=_xу=,и из соотношений (1.2) получаем _xx=_уу=_zz=-P(3+2). Так как относительное изменение объёма равно –(_xx+_уу+_zz)=-, то

=P=+23 . (1.5)

Модуль сдвига (или жесткости) равен отношению сдвигающего напряжения к деформации сдвига (см. три последних уравнения 1.2).

Приведенные зависимости используют при выводе уравнений упругой среды и, в конечном счете, для выяснения закономерностей взаимодействия твердых вполне упругих физических тел. Все эти зависимости имеют одно общее свойство – статическое происхождение.

Возникают вопросы: правомерно ли применение статических показателей деформации и упругости для случая динамического контактного взаимодействия тел? Сохранится ли предел упругости в динамике? Возможно ли осуществить сплошную деформацию сжатия свободного тела, пропорциональную действующей на него односторонней силы (воздействия)? Каков механизм трансформации линейной скорости ударника в многократно превышающую её по величине скорость звука для данной среды, которая характеризует перемещение в теле ударяемого тела возникшей волны деформаций и напряжений?

1.5.3Сила трения скольжения

Возникает при скольжении тела по поверхности другого тела

F = kR_n,

где k – коэффициент трения скольжения, зависящий от природы и состояния соприкасающихся поверхностей;
Rn – сила нормального давления, прижимающая трущиеся поверхности друг к другу. Сила F направлена в сторону, противоположную направлению движения одного тела относительно другого.

1.5.4Сила сопротивления

Действует на тело при его поступательном движении в газе или жидкости. Она зависит от скорости тела v относительно среды и направлена противоположно этой скорости

F = -kv,

где k – положительный коэффициент, храктерный для данного тела и данной среды. Зависит от скорости v , однако при малых скоростях его считают постоянным.

При взаимодействии твердых тел, как упругих, так и пластичных, при соответствующей форме ударника наблюдается проникновение его торцевой части в среду ударяемого тела и движение его относительно этой среды. Здесь также уместно задать вопрос, почему это явление игнорирует теория удара и не учитывает его в балансе энергетических потерь?

1.5.5Сила Лоренца

Действует на заряженную частицу при её движении в магнитном поле

F = qvB,

где q – заряд частицы, v – её скорость в системе отсчета, в которой индукция магнитного поля равна B. Сила Лоренца всегда перпендикулярна к вектору скорости частицы.

1.5.6К
улоновская сила

Действует между двумя заряженными частицами

где q₁ и q₂ – заряды частиц,
r – расстояние между ними,
k – коэффициент пропорциональности, зависящий от выбора системы единиц.

В отличие от гравитационной силы кулоновская сила может быть как силой притяжения, так и силой отталкивания в зависимости от знаков зарядов частиц.

1.6О понятии массы, силы и инерции

Напомним, что по представлениям Ньютона масса есть количество материи, произведение массы тела на его скорость есть свойство тела, которое характеризуется как количество движения, а приложенная сила есть действие, которое вызывает изменение состояния покоя или равномерного прямолинейного движения. И, наконец, способность свободного тела удерживать своё состояние покоя или движения обязана некоей врожденной силе материи.

Проследим ход рассуждений на эту тему И.Е.Иродова (21).

«Изучая на опыте различные движения, мы обнаруживаем, что в инерциальных системах отсчета всякое ускорение тела вызывается действием на него каких-либо других тел. Во всех случаях, когда в опыте участвуют только два тела А и В, и тело А сообщает ускорение телу В, то и тело В также сообщает ускорение телу А. Отсюда следует вывод, что действия тел друг на друга имеют характер взаимодействия. Для характеристики этого взаимодействия вводят новую фундаментальную величину – силу F, которая служит мерой механического взаимодействия тел. Поскольку сила является причиной ускорения, а ускорение обладает свойствами вектора, то постулируется, что и сила есть вектор, причём направленный так же, как и ускорение a, вызываемое этой силой F, то есть Fa.

Одной из важнейших характеристик силы является её материальное происхождение. Говоря о силе, мы всегда неявно предполагаем, что в отсутствие посторонних тел сила, действующая на интересующее нас тело, равна нулю. Если же обнаруживается, что сила действует, мы ищем её источник в виде того или иного конкретного тела или других тел.»

Далее Иродов приводит следующие соображения. В статике силу измеряют с помощью эталонной заранее отградуированной пружины, в динамике – по отношению сил к вызванным ими ускорениям F₁F₂=a₁a₂. Опыт подсказывает, что при любой по величине и направлению силе отношение Fa для данного тела остаётся постоянным. Отсюда вывод: величина Fa характеризует некоторое свойство тел, а именно, инертность, которая выражает степень неподатливости тела к изменению его скорости.

Для количественной характеристики инертности тела вводят новую физическую величину m, пропорциональную отношению Fa. Эту величину называют массой. И далее: свободная материальная точка, не подверженная действию никаких других тел, движется прямолинейно и равномерно, или, как говорят, по инерции.

Д.Б.Мэрион ( 21, стр.137):

«Для начала движения требуется большая сила, чем для поддержания движения. Мы используем термин инерция для обозначения этого свойства вещества противиться изменению своего состояния движения Масса – это свойство вещества. Масса тела является мерой количества содержащегося в нём вещества».

Л.Эйлер в своём труде «Основы динамики точки» даёт такое определение понятию инерция:

«Я указываю всеобщие законы природы, которым следует свободное тело, не подверженное действию сил. Тело подобного рода, раз оно находится в состоянии покоя, должно вечно пребывать в покое. Если же оно имело движение, оно вечно должно двигаться с той же скоростью по прямому направлению. Оба эти закона наиболее удобно можно представить под именем закона сохранения состояния. Отсюда вытекает, что сохранение состояния является существенным свойством всех тел и что все тела, пока они остаются таковыми, имеют стремление или способность навсегда сохранять своё состояние, и это есть не что иное, как сила инерции».

В повседневной практике инерцией объясняют такие явления, как стремление продолжать движение всех предметов при остановке, например, вагона; деформацию при остановке одной части тела, и возможности свободного движения другой его части. Примером могут служить также разрушения, связанные с тем, что покоящееся тело сохраняет это состояние, а взаимодействующее с ним движущееся тело внедряется в пространство первого.

В связи с изложенным возникают такие принципиальные вопросы:

Масса – это количественная характеристика материи или степень неподатливости движению?

Инерция – это дополнительное фундаментальное свойство материи, или это физическое явление, выступающее как результат динамического взаимодействия тел, имеющих реальную структуру?

Сила – это дополнительное самостоятельное свойство, или это расчетная величина, характеризующая соотношение массы и движения?

Если для начала движения требуется большая сила, чем для его поддержания, какими формулами это учитывает классическая механика и как это согласуется с требованиями её основных законов?

Формулируя возникающие вопросы при рассмотрении толкований основных законов механики разными авторами, мы не преследуем цели ни в малейшей степени усомниться в их компетенции и высоком научном уровне. Задача состоит в том, чтобы вычленить те места в научной аргументации, которые до сих пор не нашли удовлетворительного объяснения либо приняты ими как допущения, которые ещё ждут своего разрешения. Обнаженные таким способом «сомнения», возможно, помогут в дальнейшем избежать характерных заблуждений при исследовании процесса динамического контактного взаимодействия.

1.7Импульс. Закон сохранения импульса

Импульсом частицы в совремённой механике называют величину p=mv, где m – масса частицы, v – её скорость в рассматриваемой системе отсчета. Определение этой величины как количества движения, данное ей Ньютоном, принято считать устаревшим прежним её названием.

Считается, что величиной, ответственной за изменение импульса частицы, является сила, так как

dpdt=F (1.6).

Это уравнение представляет собой другую форму записи второго закона Ньютона: «производная по времени от импульса частицы равна действующей силе».

В неинерциальной системе отсчета сила F включает в себя не только силы взаимодействия, но и силы инерции. Уравнение (1.6) позволяет найти приращение импульса частицы за любой промежуток времени, если известна зависимость силы F от времени, dp=Fdt.

З
а конечный промежуток времени приращение импульса

Эту величину называют импульсом силы – приращение импульса частицы за любой промежуток времени равно импульсу силы за то же время. Если F=const, то p₂ – p₁ =Ft.

Импульс системы материальных точек p=p_i , где p_i -- импульс i-й частицы.

Импульс системы – величина аддитивная, то есть импульс системы равен сумме импульсов её отдельных частей независимо от того, взаимодействуют они между собой или нет.

И
зменение импульса системы dpdt = dp_idt. Но

г
де F_ik – силы, действующие на i-ю частицу со стороны других частиц системы (внутренние силы);
Fi – сила, действующая на эту же частицу со стороны частиц, принадлежащих другим телам, не входящим в рассматриваемую систему – внешние силы.

После подстановки последнего выражения в предыдущее

Двойная сумма – это сумма всех внутренних сил. Сумма всех внутренних попарно одинаковых сил в соответствии с третьим законом Ньютона равна нулю. Отсюда dpdt = F , где F – результирующая всех внешних сил.

Закон изменения импульса системы: производная по времени от импульса системы равна векторной сумме всех внешних сил, действующих на частицы системы.

Импульс замкнутой системы есть величина постоянная.

В качестве наглядного примера реализации третьего закона Ньютона приводят обычно случай соударения тел (шаров) с равными массами, упругими свойствами и равными противоположно направленными скоростями. В этом случае полагают, что тела обмениваются скоростями так, что m₁v₁ = m₂v₂ , откуда m₁m₂=v₂v₁. Именно справедливость этого равенства для конкретных тел экспериментально с помощью подвешенных на нитях шаров доказывал Ньютон и приходил к выводу о справедливости своего закона равенства действия-противодействия.

Рассмотрим один характерный пример логического анализа феномена «обмена скоростями» (9, 15). Пусть происходит соударение двух идентичных свободных шаров с начальными скоростями -v₁ и +v₂. Предполагается, что при соударении в упругих телах сформируются ударные импульсы, несущие соответственно количество движения m₁v₁ и m₂v₂. В результате сложения этих импульсов в каждом теле, последние получат новые скорости v₃ и v₄ (естественно, несколько отличные от первоначальных).

С
оответственно, m₂v₃ = m₂v₂ – m₁v₁и m₁v₄ = m₁v₁ – m₂v₂, откуда

Д
опустим, что взаимодействующие тела имеют единичные массы и скорости, то есть v₁ = -1 и v₂ = +1. Тогда v₃ = v₂–v₁ = +2 и v₄  = v₁ – v₂  = -2

Таким образом, в результате взаимодействия импульсов движения физически тела приобрели в некоторый момент удвоенные по модулю скорости противоположных знаков. Сложив их с действующими ранее скоростями (до удара), получим

v₁ = -1 v₃ = +1

v₂ = +1 v₄ = -1.

Произошло то, что принято называть словами: «тела обменялись скоростями».

В логической цепи хронологии события «взаимодействие» или, другими словами, истории каждого из взаимодействующих тел, мы должны предположить следующее. Если скорость тела 1 изменяется от –1 до +1, то в какой-то момент взаимодействия оно должно остановиться всеми составляющими его точками и кратковременно испытать состояние абсолютного покоя. То же нужно сказать и о теле 2. Через какой механизм это происходит? В какое время от начала взаимодействия это происходит? Где находится эта нулевая точка относительно метрики пространства рассматриваемых тел? Как это всё согласуется с законами сохранения?

Теперь появляется возможность сформулировать очередные вопросы применительно уже к положениям всего рассматриваемого раздела в целом. Утверждение, что тела до и после взаимодействия сохраняют неизменным суммарный импульс движения, равносильно утверждению, что рассматриваемая механическая система имеет коэффициент полезного действия равный единице. Правомерно ли практикуемое в теории суммирование локальных движений точек в составе тела с его движением в целом? Возможно ли говорить о равенстве действия и противодействия при разных скоростях соударяющихся тел, при разной их протяженности или разной конфигурации их головных частей? Возможен ли обмен скоростями при абсолютной твердости одной из контактных поверхностей? Как в этом случае будет функционировать сила F=ma и что ей будет противостоять? Что же, в конечном счете, определяет соотношение скоростей до и после, закон сохранения импульса или закон сохранения энергии?

Наиболее логически обоснованное приближение к ответу на поставленные вопросы даёт нам «Механика»Л.Д.Ландау и Е.М.Лифшица. Основные её положения мы будем пытаться максимально использовать в дальнейшем, акцентируя внимание на экспериментальную апробацию изложенных теоретических установок.

1.8Уравнения движения

1.8.1Обобщенные координаты

О
дним из основных понятий, которым оперирует механика, является понятие материальной точки, или, короче, частицы. Под этим названием понимают тело, размерами которого можно пренебречь при описании его движения. Положение материальной точки в пространстве определяется его радиус-вектором r ,компоненты которого с её декартовыми координатами x,у,z. Производная r по времени v=drdt называется скоростью, а вторая производная d²rdt называется ускорением точки. Дифференцирование по времени для удобства чтения обозначают точкой над символом:

Для определения положения системы из N материальных точек в пространстве надо задать N радиус-векторов, то есть 3N координат. Число независимых величин, задание которых необходимо для однозначного определения положения системы, называется числом её степеней свободы. Любые S величин q₁, q₂, …., q_s, вполне характеризующие положение системы (с S степенями свободы), называют её обобщенными координатами, а производные q_i её обобщёнными скоростями.

Одновремённое задание всех скоростей и координат полностью определяет состояние системы и позволяет в принципе предсказать дальнейшее её движение. С математической точки зрения это значит, что заданием всех координат q и скоростей q в некоторый момент времени однозначно определяется также и значение ускорений q в этот момент.

Cоотношения, связывающие ускорения с координатами и скоростями, называются уравнениями движения. По отношению к функциям q(t) это дифференциальные уравнения второго порядка, интегрирование которых позволяет в принципе определить эти функции, то есть траектории движения механической системы.

1.8.2Принцип наименьшего действия

Наиболее общую формулировку закона движения механических систем даёт принцип наименьшего действия. Согласно этому принципу каждая механическая система характеризуется определённой функцией

L(q₁,q₂,….,q_s; q₁,q₂….,q_s,t) или L(q,q,t). При этом движение системы удовлетворяет следующему условию.

П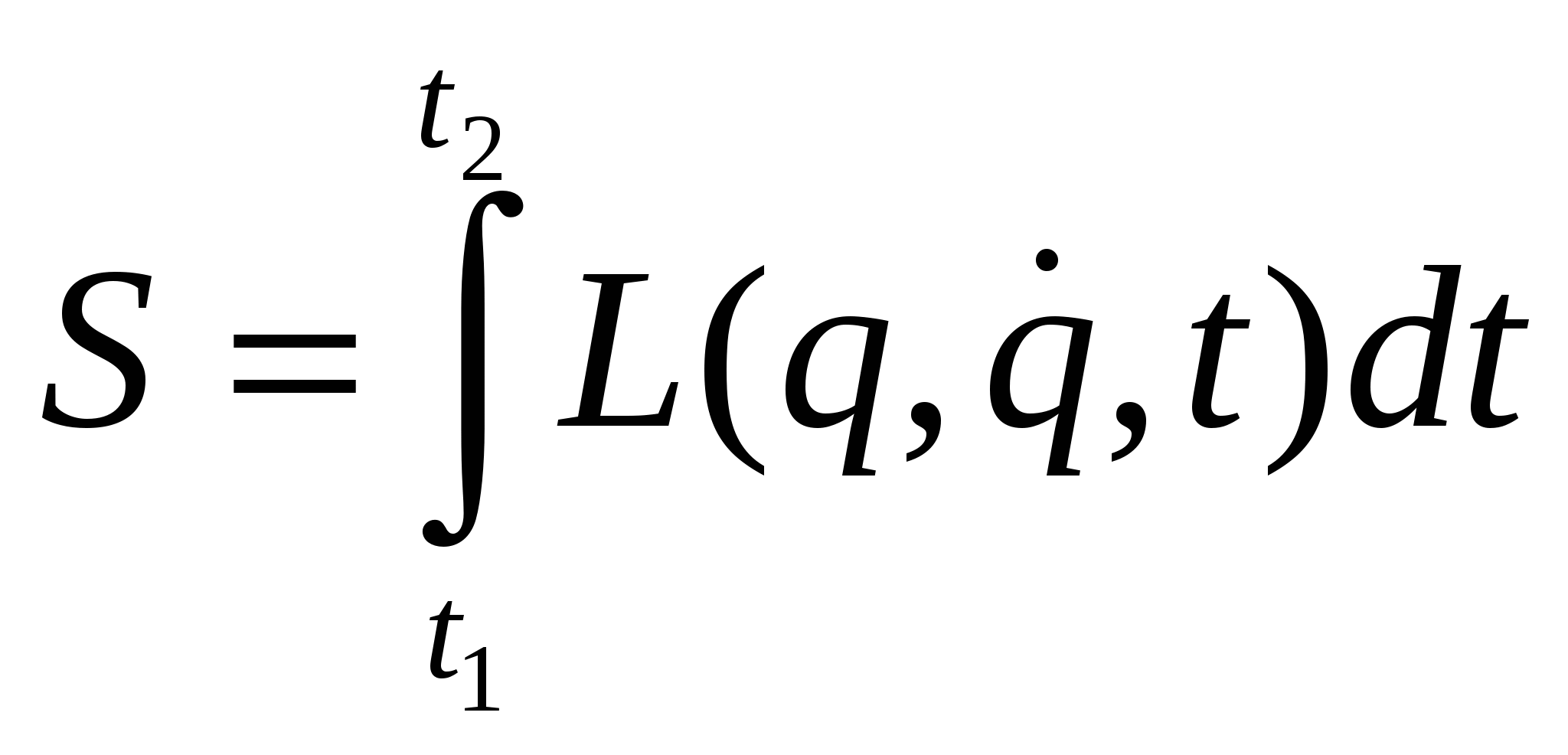
усть в моменты времени t = t₁ и t = t₂ система занимает определённые положения, характеризуемые двумя наборами значений координат q⁽¹⁾ и q⁽²⁾. Тогда между этими положениями система движется таким образом, чтобы интеграл

имел наименьшее возможное значение. Функция L называется функцией Лагранжа данной системы, а интеграл S – действием. То, что функция Лагранжа содержит только первые производные от q, указывает на то, что механическое состояние полностью определяется заданием координат и скоростей.

В
результате вывода и решения дифференциальных уравнений, определяющих минимум интеграла S, приходим к уравнению

П
ри наличии нескольких степеней свободы в принципе наименьшего действия должны независимо варьироваться S различных функций q_i(t). Тогда мы получаем S уравнений вида

Эти уравнения в механике называют уравнениями Лагранжа. Если функция Лагранжа данной механической системы известна, то эти уравнения устанавливают связь между ускорениями, скоростями и координатами, то есть представляют собой уравнения движения системы. Математически уравнения Лагранжа составляют систему S уравнений второго порядка для S неизвестных функций q_i(t). Общее решение такой системы содержит 2S произвольных постоянных. Для их определения и тем самым полного определения движения механической системы необходимо знание начальных условий, характеризующих состояние системы в некоторый заданный момент времени, например, знание начальных значений всех координат и скоростей.

1.8.3Принцип относительности Галилея

Для изучения механических явлений нужно выбрать ту или иную систему отсчета. В различных системах отсчета законы движения могут приобретать различную форму. Задача состоит в том, чтобы отыскать такую систему отсчета, в которой законы механики приобретали бы наиболее простой вид.

По отношению к произвольной системе отсчета пространство является неоднородным и неизотропным. Это значит, что если какое-либо тело не взаимодействует ни с какими другими телами, то, тем не менее, его различные положения в пространстве и его различные ориентации в механическом отношении не эквивалентны. То же самое относится в общем случае и ко времени, которое будет неоднородным, то есть его различные моменты неэквивалентными. Усложнения, которые вносили такие свойства пространства и времени в описании механических явлений, могут быть значительными. «Кажущееся» движение тел в произвольной системе привело бы к неверным выводам о его действительной траектории перемещения и характере взаимодействия с другими телами. Свободное в пространстве тело, не подвергающееся внешним воздействиям, не могло бы покоиться: если скорость тела в некоторый момент времени и равна нулю, то уже в следующий момент тело начало бы двигаться в некотором направлении.

Но всегда можно найти такую систему отсчета, по отношению к которой пространство было бы однородным и изотропным, а время однородным. В ней свободное тело, покоящееся в некоторый момент времени, остаётся в покое неограниченно долго или продолжает равномерное прямолинейное движение. Такая система называется инерциальной.

О виде функции Лагранжа свободно движущейся материальной точки в инерциальной системе отсчета можно сказать следующее. Однородность пространства и времени означает, что эта функция не может содержать явным образом ни радиус-вектора r точки, ни времени t, и потому L является функцией лишь скорости v. В силу же изотропии пространства функция Лагранжа не может зависеть также и от направления вектора v, и является функцией лишь от его абсолютной величины, то есть от квадрата V²=v². Отсюда^: L=L (v²).

В
виду независимости функции Лагранжа от r имеем Lr = . Поэтому уравнение Лагранжа приобретает вид

Откуда Lv = const. Но поскольку Lv является функцией только от скорости, то отсюда следует, что и V = const.

Если наряду с имеющейся инерциальной системой отсчета ввести другую, движущуюся относительно первой прямолинейно и равномерно, то законы свободного движения по отношению к введенной системе будут те же, что и по отношению к первоначальной: свободное движение снова будет происходить с постоянной скоростью. Во всех подобных системах свойства пространства и времени одинаковы и одинаковы все законы механики. Это утверждение составляет смысл и содержание принципа относительности Галилея.

1.8.4Функция Лагранжа свободной материальной точки

Рассмотрим простейший случай – свободное движение материальной точки относительно инерциальной системы отсчета. Для выяснения вида функции Лагранжа используют принцип относительности Галилея. Если инерциальная система отсчета K движется относительно инерциальной системы отсчета Kс бесконечно малой скоростью , то v= v + . Так как уравнения движения во всех системах отсчета должны иметь один и тот же вид, то функция L(v²) должна при таком преобразовании перейти в функцию L, которая имеет вид

L = L(v²) = L(v² + 2v + ²).

Разлагая это выражение в ряд! по степени и пренебрегая бесконечно малыми высших порядков, получим:

L(v²) = L(v²) = L(v²) + Lv² 2v .

Второй член первой части этого равенства будет полной производной по времени только в том случае, если он зависит от скорости v линейно. Поэтому Lv² от скорости не зависит, то есть функция Лагранжа в рассматриваемом случае прямо пропорциональна квадрату скорости

L = av² .

Из того, что функция Лагранжа такого вида удовлетворяет принципу относительности Галилея в случае бесконечно малого преобразования скорости, непосредственно следует, что функция Лагранжа инвариантна и в случае конечной скорости V системы отсчета K относительно K. Действительно

L= L + ddt(2arV + aV²t).

В
торой член является полной производной и может быть опущен. Постоянную a принято обозначать как m2, так что окончательно функция Лагранжа свободно движущейся точки

В
еличину m называют массой материальной точки. В силу свойства аддитивности функции Лагранжа, для системы невзаимодействующих точек имеем

Лишь при учете свойства аддитивности данное определение массы приобретает реальный смысл.

1.8.5Функция Лагранжа системы материальных точек

Рассмотрим систему материальных точек, взаимодействующих друг с другом в рамках системы при отсутствии взаимодействия со стороны точек, находящихся за пределами системы. Такую систему называют замкнутой.

В
заимодействие между материальными точками может быть описано прибавлением к функции Лагранжа невзаимодействующих точек определенной, зависящей от характера взаимодействия функции координат. Обозначив эту функцию через -U, можем записать

где r_a – радиус –вектор a-той точки.

Это общий вид функции Лагранжа замкнутой системы. Сумму

называют кинетической энергией, функцию U называют потенциальной энергией системы.

На основании того, что потенциальная энергия зависит только от расположения всех материальных точек в один и тот же момент времени, предполагается, что изменение положения одной мгновенно отражается на всех остальных.

В
ид функции Лагранжа показывает, что время не только однородно, но и изотропно, то есть его свойства одинаковы по обоим направлениям. Замена t на -t оставляет функцию Лагранжа, а, следовательно, и уравнения неизменными. Другими словами, если в системе возможно некоторое движение, то всегда возможно и обратное движение – такое, при котором система проходит те же состояния в обратном порядке. В этом смысле все движения, происходящие по законам классической механики, обратимы. На основе функции Лагранжа можно составить уравнение движения

П
осле соответствующей подстановки получаем

Уравнения в этой форме называются уравнениями Ньютона и представляют собой основу системы взаимодействующих частиц.

В
ектор

называется силой, действующей на a-тую точку. Вместе с U она зависит лишь от координат всех частиц, но не от их скоростей. Приведенные уравнения также показывают, что и векторы ускорения частиц являются функциями только от координат.

Потенциальная энергия есть величина, определяемая лишь с точностью до прибавления к ней произвольной постоянной; такое прибавление не изменило бы уравнений движения. Наиболее естественный и обычно принятый способ выбора этой постоянной заключается в том, чтобы потенциальная энергия стремилась к нулю при увеличении расстояний между частицами.

Взаимодействие систем. Рассмотрим незамкнутую систему А, взаимодействующую с другой системой В, совершающей заданное движение. В таком случае говорят, что система А движется в заданном внешнем поле, создаваемом системой В. Поскольку уравнения движения получаются из принципа наименьшего действия путём независимого вариирования каждой из координат (то есть как бы считая остальные известными), мы можем для нахождения функции Лагранжа L_А системы А воспользоваться лагранжевой функцией L всей системы А+В, заменив в ней координаты q_В заданными функциями времени.

П
редполагая систему А+В замкнутой, будем иметь:

г
де первые два члена представляют собой кинетические энергии систем А и B, а третий член – их совместную потенциальную энергию.

Подставив вместо q_В заданные функции времени и опустив член T(q_B(t),q_B(t), зависящий только от времени и поэтому являющийся полной производной от некоторой функции времени, получим

То есть, движение частицы во внешнем поле описывается функцией Лагранжа обычного типа с тем отличием, что потенциальная энергия может зависеть от времени явно.

Д
ля движения одной частицы во внешнем поле общий вид функции Лагранжа

и
уравнение движения

1.9Движение тела с переменной массой

При реализации процессов, связанных с движением тела, часто возникает ситуация, при которой одновремённо с движением происходит непрерывное присоединение массы или, напротив, её убыль. Например, вибротранспортирование сыпучих грузов, загрузка конвейера из неподвижного бункера, старт ракеты, полёт реактивного самолёта или другие подобные процессы.

Рассмотрим особенности такого движения и характеризующие его величины. Пусть в некоторый момент времени t масса движущегося тела А равна m, а присоединяемая (или отделяемая) масса имеет скорость u относительно данного тела.

Введём вспомогательную инерциальную К-систему отсчета, скорость которой равна скорости тела в данный момент времени t. Это значит, что в момент t тело А покоится в К-системе.

Пусть за промежуток времени от t до t+dt тело А приобретёт в К-системе импульс mdv. Этот импульс тело получает за счёт действия силы F со стороны окружающих тел или силового поля, а также за счет присоединения (отделения) массы m, которая приносит (уносит) импульс mU. В результате получаем:

mdv = Fdt mu .

Имея ввиду, что m есть приращение dm, предыдущее выражение можно записать как

m
dv = Fdt dmu , или

где u – скорость присоединяемого вещества относительно рассматриваемого тела.

Это уравнение является основным уравнением динамики материальной точки с переменной массой и носит имя Мещерского. Будучи полученным в одной инерциальной системе отсчета, это уравнение в силу принципа относитеьности справедливо и в любой другой инерциальной системе. Если же система отсчета неинерциальна, то под силой F следует понимать результирующую как сил взаимодействия данного тела с окружающими телами, так и сил инерции.

П
оследний член уравнения (1.6) называется реактивной силой

Уравнение Мещерского по своей форме совпадает с основным уравнением динамики материальной точки постоянной массы: слева – произведение массы тела на ускорение, справа – действующие на него силы, включая реактивную силу. Однако в случае переменной массы мы не можем внести массу m под знак дифференциала и представить левую часть уравнения как производную по времени от импульса, так как

В частном случае, когда u = -v , то есть присоединяемая масса неподвижна в интересующей нас системе отсчета или отделяемая масса становится неподвижной в э
той системе, то уравнение (1.6) принимает следующий вид:

Данное уравнение применимо в случае движения платформы, нагружаемой сыпучим веществом из неподвижного бункера.

Глава 2
О природе движения

Глубокое понимание природы взаимодействий невозможно без четкого определения понятия движение.

Украинский энциклопедический словарь даёт такое определение ( стр.502): «Движение – способ существования материи, её неотъемлемое свойство. Движения без материи не существует так же, как материя без движения. В этом состоит абсолютный характер движения. Покой, равновесие, равнодействие относительны. Движение является сущностью пространства и времени как форм существования материи».

Надо полагать, что приведенная формулировка в энциклопедическом издании последних лет отражает совремённые научные и философские воззрения на предмет нашего рассмотрения. С другой стороны, она не может служить опорной конструкцией для понимания внутренней природы таких явлений, как столкновения, удар, вибрация, извержение, общим знаменателем которых является движение материальных субстанций.

Приведенные философские суждения практически не могут служить базой для конкретных исследований и экспериментов, так как не затрагивают физическую сущность движения в реальном измерении и реальном масштабе времени.

Утверждение, что движение является неотъемлемым свойством материи, звучит несколько противоречиво для механики, которая рассматривает поведение конкретных предметов.

Как свидетельствует повседневный опыт, именно материальные объекты демонстрируют нам свою способность воспринимать движение, отдавать движение и, в общем случае, обмениваться движением. Начиная с Ньютона и Гюйгенса, теоретическая механика провозглашает: твёрдые тела при прямом столкновении обмениваются скоростями и разлетаются в разные стороны. Но, если в процессе «разлёта» тела изменяют свою первоначальную скорость на противоположную, значит, в процессе своей механической эволюции они проходят через состояние покоя (нулевую скорость) и при этом продолжают существовать как материальные объекты.

Ещё поразительней выглядит способность промежуточных тел в системе сохранять своё состояние покоя при ударе по системе и при этом передавать энергию движения крайнему телу в системе.

Возникновение противоречий в суждениях, приведенных выше, можно объяснить тем, что философия рассматривает всеобщие закономерности мира и исходит из концепции неистребимости энергии в микро и макро масштабе. Механика же изучает закономерности движения и взаимодействия материальных объектов в суженых масштабах избранных для рассмотрения систем отсчета, как правило, игнорируя внутреннюю динамику вещества, начиная с молекулярного уровня, и внешнюю динамику в планетарном понимании. Эти условия обычно принимаются как стационарные, наперед заданные и не влияющие существенно на исследуемые взаимодействия.

Тот же раздел теоретической механики, который оперирует понятиями материальной точки, относительного движения, обобщенных координат, фиктивных и консервативных сил, можно было бы охарактеризовать как виртуальный. Полученные виртуальные выводы эта наука впоследствии обращает на реальные тела и процессы. Методы виртуальной механики весьма эффективны, экономны в расчетах, имеют высокий уровень научной абстракции, но весьма опасны отклонениями от истинного положения вещей.

2.1Ещё раз о некоторых исходных положениях динамики

Любое физическое тело – это пространственная конструкция, все материальные точки которой находятся на связи и имеют одинаковые скорости.

Система обособленных физических тел, находящихся на связи в ограниченном этими же связями пространстве, представляет собой механическую систему, агрегат или просто механизм.

В этом плане любое твёрдое тело можно интерпретировать как обособленную механическую систему или совокупность материальных точек, находящихся на связи, занимающую определённый объём в пространстве. Возможно, здесь есть смысл вернуться к понятию «места в пространстве», которым оперировал Ньютон: «Место есть часть пространства, занимаемая телом и, по отношению к пространству, бывает или абсолютным или относительным. Я говорю часть пространства, а не положение тела и не объемлющую его поверхность».

Обособленное тело имеет собственное пространство, ограниченное его свободными поверхностями, и объём, величина которого определяется параметрами этих поверхностей. Соответственно, это тело в данный момент времени, находясь в свободном окружающем пространстве, вытесняет свой объём из общего объёма пространства, как, например, шар, опущенный в сосуд с водой. Если же рассматриваемое тело изменяет своё положение в пространстве, то его перемещению будет сопутствовать также перемещение в тех же координатах места, которое будет освобождать движущееся тело. Здесь мы наблюдаем явление, подобное дырочной проводимости в полупроводниках. Движение «места», в котором ничего нет, мы должны признать как реальный физический процесс, который, как и всякий другой, может быть идентифицирован устойчивыми и повторяющимися симптомами.

В силу того, что связи неизменны и векторы скоростей всех точек согласованы по направлению, свободное твердое тело в каждый данный момент времени может совершать только прямолинейное и равномерное движение в пространстве. Тело не может двигаться одновремённо вперёд и назад, вверх, вниз и т.д.

Если на одно и то же тело действуют несколько сил, которые могут инициировать другие тела или силовые поля, то на рассматриваемое тело будет действовать векторная равнодействующая сила. Эта равнодействующая станет причиной нового движения, которое будет отличаться направлением и, в общем случае, интенсивностью (скоростью).

В результате своего движения тела оставляют свой след в плоскости или объёме пространства. Этот след мы называем траекторией.

Следовательно, свободное движение в его физической интерпретации может быть только равномерным и прямолинейным. Траектория, воспринимаемая визуально и воображаемая абстрактно, выступающая как результат изменения в каждый момент времени направления движения, может быть произвольной формы. Вектор движения в любой точке траектории совпадает с касательной к кривой, изображающей эту траекторию.

Движение как таковое характеризуется направлением и интенсивностью (скоростью), изменение скорости в каждую единицу времени называют ускорением. В таком понимании параметры движения могут быть применимы как к материальным объектам перемещения, так и к нематериальным, например, перемещению светового пятна, тени и т.п.

В

случае реальных материальных объектов, обладающих массой вещества, вводят понятие количества движения

где m – масса тела,
v – скорость его движения.

Величину p в механике принято называть импульсом движения

Величина p характеризует потенциальную возможность движущегося в пространстве тела оказывать силовое воздействие на другое тело в случае их встречи (динамического контактного взаимодействия).

И
зменение во времени величины и направления скорости тела характеризует его ускорение

В
свою очередь изменение количества движения тела при воздействии на него другого тела, как показано выше, связывают с действующей силой

Под понятием свободное пространство мы будем подразумевать гипотетический объём, который охватывает тело за его границами и который характеризуется тремя взаимно перпендикулярными осями координат (метрикой пространства). При этом полагаем, что он лишен каких-либо материальных включений и действия силовых полей. Мы не знаем, допускает ли природа существование такого состояния. Но такая научная абстракция может быть допущена. Если заранее точно известно, что на исследуемые динамические характеристики присутствие посторонних предметов и материальных включений существенного влияния не оказывает.

В таком понимании можно говорить, что пространство есть физическая реальность, обладающая протяженностью и объёмом в координатах отсчета. При этом по условиям задачи этот объём может быть абсолютно свободным от какой-либо материи или заполненным равномерно распределённым веществом (газом, жидкостью, пластичным заполнителем и т.п.). Материальное пространство в отличие от свободного кроме метрических показателей может иметь также физические, такие, как плотность, вязкость, упругость и тому подобное. Кроме того, оно может быть изотропным, анизотропным, однородным и неоднородным. Примером движения в материальном пространстве может служить процесс внедрения одного тела в пространство другого во время их соударения.

Теоретическая механика оперирует такими понятиями, как абсолютно твёрдое тело, материальная точка, частица.

Абсолютно твёрдое, или, в общем, твёрдое тело – это система материальных точек, расстояние между которыми не меняется в процессе движения тела в целом. Реальное тело можно считать абсолютно твёрдым, если в условиях рассматриваемой задачи его деформации пренебрежительно малы. Однако такое допущение не может применяться тогда, когда рассматривается динамическое контактное взаимодействие (удар).

Конкретное тело характеризуется параметрами, по которым его можно идентифицировать: линейными и объёмными показателями, конфигурацией, плотностью, упругостью или пластичностью составляющего его вещества и так далее.

В тех случаях, когда размерами и массой тела можно пренебречь, используют понятие материальная точка или частица. В частности, это понятие используется при выводе основных уравнений движения не связанных между собой свободных в пространстве объектов: планет, комет, межпланетных станций и т.п. Если же в процессе рассмотрения появляются движения, которые влияют на внутреннюю организацию твердых тел, то дальнейшее рассмотрение их состояния и поведения следует проводить на основе реальных параметров: массы, протяженности, конфигурации, плотности и т.д.

Локальные изменения размеров, конфигурации или смещения одних групп материальных точек относительно других являются процессами внутренними, принадлежащими данному телу, и их рассматривают в системе координат, связанной с этим телом.

Как показывает повседневный опыт и результаты экспериментов, при столкновении твёрдых тел каждое из них представляет для другого непреодолимое препятствие, по крайней мере, в течение времени, на протяжении которого они сохраняют свою целостность.

Р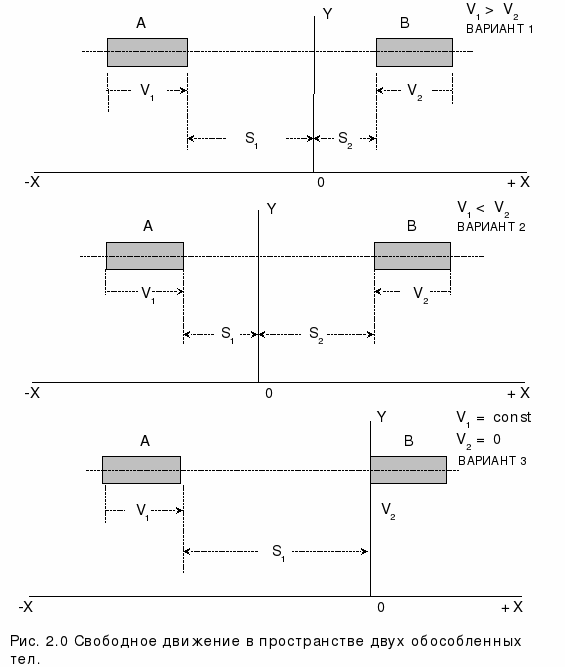
ассмотрим пример свободного движения в пространстве обособленного тела, приведенный на рисунке 2.1. Пусть в свободном от любых посторонних влияний пространстве из позиций А и В движутся навстречу друг другу два твёрдых и достаточно упругих тела. Их движение реализуется вдоль общей оси так, что обеспечивается лобовое столкновение и прямой удар.

Вариант 1.

Известно, что V₁ > V₂ , известны численные значения скоростей и протяженность разделяющего тела пространства S. Тогда из соотношений S₁=V₁; S₂=V₂ и S₁S₂ = V₁V₂ мы можем рассчитать положение точки на оси X, а, значит, и положение плоскости встречи У.

Пока тела движутся по заданной оси, проведём вправо и влево от плоскости У через равные промежутки расстояния S мерные отрезки S. Таким образом мы создадим метрику пространства, в котором разворачивается исследуемое событие. Из повседневной практики известно, что после встречи тела «на короткий промежуток» останавливаются, а затем «разлетаются» в противоположные стороны в соответствии с усвоенным ими в результате взаимодействия количеством движения. Так как тела по отношению друг к другу проявили себя как непреодолимое препятствие, то точка 0 может служить истинной границей начала движения после соударения. В целом система координат X0У (для упрощения – в плоском изображении), одновремённо неподвижная относительно обоих тел, является той универсальной системой, которая позволяет осуществить наблюдение и анализ процесса динамического контактного взаимодействия в его трёх основных фазах:

1)предударный период; 2)собственно удар; 3)послеударный период.

Приведенная система координат позволяет непосредственно анализировать процесс движения в реальном масштабе времени и пространства.

Вариант 2 показывает, что при изменении соотношения скоростей соответственно изменяется положение в пространстве нулевой координаты у, но сохраняются динамические параметры тел и картина их соударения.

Вариант 3 показывает, что при одном покоящемся теле и другом движущемся плоскость встречи у совмещается с передним торцом неподвижного тела.

Общим для всех трёх вариантов является то обстоятельство, что независимо от своей скорости тело А по отношению к телу В одинаково успешно выполняет функцию эталона. Разница состоит только в положении нулевой плоскости связанной системы координат.

Внимательный анализ приведенных графиков позволяет сделать некоторые принципиальные выводы о природе движения.

Движение – это свойство или способность любого материального субъекта природы самопроизвольно в соответствии с усвоенной им скоростью изменять своё положение в пространстве вдоль оси, предписанной ему предшествующим или действующим фактором.

С другой стороны, в силу своей «конструктивной природы», тело не может самопроизвольно изменить интенсивность своего движения. Это обусловлено тем, что все составляющие его точки находятся в симметричной связи, и все внутренние силы уравновешены. В этом случае говорят о сохранении импульса движения.

Изменение интенсивности движения, таким образом, может быть вызвано только внешним по отношению к телу фактором. И этим фактором может быть только другое тело.

Тела взаимодействуют либо при непосредственном контакте, либо посредством силового поля. Содержательным примером такого поля является сила всемирного тяготения тел друг к другу.

Появление второго тела вносит определённость в логику дальнейших рассуждений. Оно позволяет сотворить законченную систему идентификации движения. Оно же, как всякий эталон, выполняет свою служебную функцию и даёт дорогу дальнейшим суждениям и заключениям. Без эталона невозможно определить ни один из физических факторов: размер, объём, температуру, цвет и т.д.

Анализируя приведенные графики, мы приходим к очень важному выводу. Движение как процесс пересечения линий метрики пространства принадлежит исключительно телу В и не зависит от присутствия или отсутствия других тел в окружающем пространстве. Это нашло отражение даже в стилистике нашего языка: раньше говорили «движущее ся тело». Импульс движения, сосредоточенный в массе тела, перемещается в пространстве и ждет своего часа, чтобы выявить себя в поведении тела, которое окажется на его пути.

Движение, которое тело совершает относительно метрики пространства, является его собственным движением.

Собственное движение тела может быть выявлено с помощью другого тела с произвольными параметрами и взаимосвязанной неподвижной относительно обоих тел системы координат.

Как показывает схема по Варианту 3, тело может иметь нулевую собственную скорость и покоиться в пространстве.

Удерживаясь на позициях принятой логики суждений, мы уже не можем, как ранее, утверждать, что с телом, которое свободно и равномерно движется в пространстве, ничего физически не происходит. Если тело движется, значит, оно существует. Непосредственно после взаимодействия и выхода на новую скорость оно совершает гармонические колебания вдоль и поперёк собственной оси, и это никак не мешает ему двигаться прямолинейно и равномерно. Находясь в определённой точке реального силового поля, оно вызывает возмущение пространства в этой точке. Двигаясь, оно обеспечивает перемещение этого возмущения в координатах пространства. Движущееся тело по сравнению с подобным покоящимся, обладает вполне определённым двигательным потенциалом. За счет внутренней энергии и своих внутренних эволюций оно способно излучать тепловую и электромагнитную энергию и одновременно перемещать в пространстве координату этих излучений. Перемещаясь, тело выполняет информационную работу в виде присутствия или отсутствия в определённых точках, движения тени и тому подобное. Наконец, за счет своих собственных внутренних ресурсов свободное тело может распадаться на произвольное число составных частей, каждая из которых приобретает новые, не сопоставимые с предшествующими, показатели как импульса, так и скорости движения. И в этой ситуации оно уже не сохраняет сообщенного ему импульса движения, а без воздействия извне порождает новые. Но баланс суммарной энергии, естественно, сохраняется. А сам факт распада находится в ряду событий, которые сопровождают свободно движущееся тело. Процесс распада свободного тела является процессом принципиально необратимым. Возврат всех точек на прежние связи немыслим, поскольку часть энергии при распаде безвозвратно рассеялась на побочные явления, напрямую не связанные с процессом механического движения.

Двигаясь (перемещаясь) в пространстве, материальное тело реализует вполне определённый физический процесс и одновремённо является субъектом этого процесса.

Утверждают, что, находясь внутри движущегося объекта (вагона, судна, самолёта), мы никак не сможем определить его скорость и направление движения. И это якобы служит убедительным доказательством того, что всякое движение относительно. Но мы с таким же успехом не сможем определить и другие показатели объекта: его цвет, конфигурацию, состояние поверхности и т. д. Наша метрологическая несостоятельность никак не отразится на состоянии тел: они будут «сохранять» данные им природой отличия.

Следует отличать движение тела как такового в координатах окружающего его пространства (когда скорости всех его точек неизменны) и движение (смещение) отдельных его объёмов в координатах (пространстве) рассматриваемого тела.

Местные смещения сечений и объёмов относятся к внутренним движениям в механической системе тела и на его скорость в целом влиять не могут. Изменить скорость тела в целом (при сохранении его целостности) могут только согласованные смещения всех его точек на протяженности тела, а реализовать это возможно только путём внешнего воздействия.

Рассматривая положение тела в пространственной системе координат, необходимо строго соблюдать генеральное условие механики: говорить о движении тела можно только тогда, когда все его точки начнут согласованное движение в одном направлении. То есть, всякие другие движения, не охватывающие всю массу в целом (продольные, поперечные, возвратно-поступательные и иные), не могут суммироваться с объёмным движением тела, и должны быть отнесены к местным деформациям.

Если из десяти последовательных сечений тела согласованно сместились, например, вперёд только девять, то у нас нет никаких оснований предполагать о начале движения тела в целом, и речь может идти только о деформации тела. И только в тот момент, когда к девяти предыдущим присоединится десятое, возникает эффект движения тела в целом.

Такой подход к определению природы движения хорошо согласуется с определением, сформулированным М.В.Ломоносовым ещё в 18-том столетии:

«Так как тела могут двигаться двояким движением – общим, при котором всё тело непрерывно меняет своё место при покоящихся друг относительно друга частях, и внутренним, которое есть перемена места нечувствительных частиц материи».

На основании всего выше изложенного, можно сделать вывод о том, что движение тела, имеющего реальную массу и протяженность, возникает как суммарный эффект от всех механических эволюций, предшествующих началу движения. В этом плане было бы неверным судить о начале движения по смещению переднего или заднего торцов тела и даже центра его тяжести. И здесь на помощь приходит понятие материальной точки, наделённой всей массой, объёмом и обладающей вырожденными координатами протяженности.

Ещё древнегреческий философ Аристотель (384 – 322г. до н.э.) механические перемещения делил на два типа: «естественные» и «насильственные». Под естественным подразумевалось движение небесных тел, отвесные движения вверх-вниз и т.д. Насильственным считалось движение под действием других тел – «двигателей». В такой классификации просматривается некий физический смысл. Опираясь на совремённые представления динамики, эти представления можно было бы изложить в следующей редакции.

Любое обособленное в пространстве тело может находиться в состоянии покоя или прямолинейного равномерного движения в соответствии с унаследованным им количеством движения. Такое движение можно было бы назвать собственным движением тела.

Любое обособленное тело, находящееся на связи в составе агрегата или механической системы, неотделимо от системы и находится в движении, совокупном с системой. Движение, которое тело совершает в составе механической системы, можно было бы охарактеризовать как движение переноса. Движение переноса – всегда вынужденное движение.

Снаряд или ракета, выпущенные в свободное пространство, совершают собственное движение и при встрече с таким же свободным телом или, скажем, противоракетой взаимодействуют с ним в соответствии с собственными параметрами (массой, скоростью, протяженностью). В реальных условиях земного тяготения траекторию движения тела будут определять суммарный собственный импульс движения и сила земного притяжения. В результате вектор равнодействующей силы будет непрерывно изменяться, и тело опишет в пространстве криволинейную траекторию.

Груз или пассажиры в вагоне, судне или самолёте находятся в состоянии движения переноса. Их перемещение синхронно и синфазно изменяются в соответствии с эволюциями несущей их механической системы. При этом передача воздействий от системы к конкретному телу осуществляется через связи, путём возникновения или исчезновения этих связей. Если система замкнута, многосторонние связи сбалансированы, то все движения заключенных в её пределах тел при столкновении системы с препятствием или изменении её скорости, будут определяться кинематикой системы. Если же тело находится в односторонней связи с системой (пассажиры трамвая), то при остановке или торможении системы тело сходит со связи и приобретает свободное движение в пространстве. Но так как пространство системы ограничено оболочкой, то тело снова выходит на связь и снова возвращается в состояние движения переноса, отдавая избыток количества движения системе. Это хорошо ощущается при транспортировке жидкости в автоцистернах.

Каждый, кто имеет дело с молотком и наковальней, знает, что существует определённая разница при ударе бойком со свободного полёта и при удержании его в конечной позиции с помощью рукоятки.

Приведенные суждения и примеры приводят к заключению, что одно и то же тело в состоянии собственного движения и движения переноса испытывает неадекватные физические состояния, как в стационарных условиях, так и в переходных режимах.

Глава 3 Удар. Динамическое контактное взаимодействие

3.1Краткая история проблемы

Под понятием удар механика подразумевает сам факт столкновения двух и более объектов и сопутствующие этому факту физические процессы, связанные со структурными сдвигами в пространстве рассматриваемых тел, а также с изменениями их положения во внешнем поле. Исторически сложилось так, что классическая механика в своём развитии пошла вперёд, используя в своих исследованиях удар как инструмент и одновремённо игнорируя внутреннюю природу этого явления. Это позволило, не ожидая, когда появятся совершенные средства измерения, найти ответ, как ведут себя тела при взаимодействии, не задаваясь вопросом почему?

Реальные движения и эволюции тел при взаимодействии настолько сложны, скорость распространения воздействий внутри твёрдых тел настолько высока и недоступна для непосредственного измерения известными измерительными средствами, что для вывода общих закономерностей движения классическая механика вынуждена была ввести ряд упрощений и абстракций. Главные среди них – понятия материальной точки и абсолютно твердого тела.

Представление об абсолютно твёрдом теле позволило считать, что любая сила, напряжение, импульс, или, в общей форме, информация о любом событии на одном участке тела распространяются по всему телу с бесконечной скоростью (принцип дальнодействия). На основе этих представлений Ньютоном были сформулированы основные законы механики. Отличительная особенность методики установления этих законов состоит в том, что она базируется на экспериментальных результатах, полученных путем анализа поведения тел с известными параметрами до взаимодействия и после взаимодействия, минуя этап их физического состояния во времени и пространстве в период между этими двумя моментами.

Таким образом, возникла возможность с высокой степенью приближения сформулировать положение о поведении материальных объектов после взаимодействия, не рассматривая физику таких явлений, как динамический контакт, деформация и её развитие, трансформация кинетической энергии, каждое из которых характеризуется высокой скоростью протекания. Что, естественно, не могло не сказаться на отставании в развитии теории удара.

Характерной особенностью комплекса физических явлений, которые принято называть одним словом удар, является мгновенное возникновение состояния механического контакта между движущимися телами. Какой бы большой или бесконечно малой ни была скорость сближения тел, в момент, когда координата разделяющего их пространства x принимает нулевое значение, практически мгновенно возникает некоторое физическое явление, которое мы именуем «контакт». Cтрого говоря, динамический контакт тел с разными относительными скоростями возникает за время, величина которого стремится к нулю.

И какие бы размеры не имели взаимодействующие тела, макроскопические или микроскопические, чтобы изменить их движение, динамическое воздействие должно охватить всю их массу, начиная с элементарного уровня строения материи, ибо нельзя изменить движения тела в целом, не изменив в этом же направлении движение всех составляющих его частей или элементарных точек. Такова одна из величайших аксиом механики.

Исторически сложилось так, что теория удара выделилась как бы в отдельную дисциплину в рамках теоретической механики, и вокруг этой дисциплины сосредоточились особо заинтересованные теоретики и квалифицированные практики. Фундаментальная же наука о движении продолжает обходить стороной природу динамического контактного взаимодействия.

Несмотря на это, практическое применение ударных явлений выдвигает всё больше вопросов, и количество исследований в этой области бурно растёт. На это обращал внимание Н.А.Кильчевский ( ): ещё в пятидесятых годах И.Бреннан в библиографии по теории удара и вызванных ударом колебаний приводит 1800 наименований теоретических и экспериментальных исследований. Особо возрос интерес к данной тематике в послевоенные годы со стороны военных и специалистов, занятых исследованием прочностных свойств материалов.

3.2Основные фундаментальные теории удара

Рассмотрим основные фундаментальные теории, которыми пользуются в зависимости от обстоятельств и постановки задачи для выяснения количественных характеристик и физики явления удара.

Элементарная теория соударений Ньютона основана на использовании коэффициента восстановления скорости при ударе. Предполагалось, что коэффициент восстановления зависит исключительно от внутренних свойств вещества соударяющихся тел и не зависит от кинематических характеристик движения тел в момент, предшествующий удару.

Для двух поступательно движущихся тел с относительными скоростями V_Aи V_B пропорциональность между скоростями до и после удара выражается формулой

V_A+ - V_B+ = - R (V_A- - V_B-),

где R – коэффициент восстановления.

Случай R = 1 абсолютно упругим ударом; R = 0 абсолютно неупругим ударом, а все промежуточные – неупругим ударом. То есть, коэффициент восстановления используют как интегральную, осредненную характеристику вещества тел, на основе которой можно прогнозировать их поведение в случае динамических взаимодействий.

Со временем выяснилась ограниченность областей достоверного использования коэффициента восстановления, его физическая несостоятельность, несмотря на возможность сравнительно элементарными средствами получать пригодные к практическому применению результаты для исследования явлений удара в элементах конструкций.

Более критический подход позволил Е.В.Александрову (9) прийти к заключению, что «коэффициент восстановления при упругом ударе является величиной расчетной и зависящей, в первую очередь, от формы тел и их массы».

По мере развития теории упругости появились новые возможности исследования динамики упругих тел, которые были недоступны в догуковскую эпоху. Впервые методы теории упругости применили для изучения соударения твёрдых тел Навье, Сен-Венан и некоторые другие ученые. Нужно отметить, что в их экспериментах предпочтение отдавалось образцам в форме стержней различной длины и формы.

Теория Сен-Венана опирается на представление о движении внутри вещества соударяющихся стержней волн смещений и напряжений и называется волновой теорией удара.

Теория Сен-Венана предполагает, что динамическое деформиование охватывает соударяющиеся тела в целом. Эту теорию широко использовал Г.Кольский (8) для построения физической картины формирования и прохождения через твёрдые тела волн напряжения, а также для объяснения результатов оригинальных опытов Б.Гопкинсона по изучению воздействия на стержни ударных явлений типа взрыва.

Применение «волновых решений» Сен-Венана последующими исследователями часто приводило к расхождению теоретических и экспериментальных результатов некоторых параметров удара, в частности, времени соударения.

Б.М.Малышев ( 35 ) замечает:

«По поводу теории Сен-Венана о соударениях, как правило, во всех работах делается оговорка, что данная теория не подтверждается рядом опытов (Фойгт, Гамбургер и др)».

Но в этой же работе автор на собственном опыте демонстрирует, что при тщательной постановке эксперимента, результаты получаются близкие к удовлетворительным.

Теория Герца по содержанию диаметрально противоположна теории Сен-Венана. Если теория Сен-Венана предполагает охват динамическим деформированием соударяющихся тел в целом, то согласно Герцу эффекты, характеризующие развитие удара, охватывают лишь небольшую область внутри тел, примыкающую к поверхности динамического контакта. Предполагается, что остальные части соударяющихся тел не деформируются при ударе и движутся как абсолютно твердые тела. То есть, пренебрегая колебаниями, Герц свел задачу об ударе к задаче сжатия взаимодействующих тел. Модель соударения реальных тел свелась к соударению двух материальных точек, разделённых находящимся между ними упругим элементом.. Динамическое силовое взаимодействие соударяющихся тел далее определяется по разработанной Герцем теории контактных взаимодействий между прижимаемыми упругими телами.

Своеобразие ситуации, возникшей в связи с существованием этих двух теорий, хорошо охарактеризовал Б.М.Малышев (35):

«В теории удара упругих тел создалось положение, когда одни исследователи, начиная с Герца, утверждают и показывают, что при соударении трехмерных упругих тел волновыми эффектами можно пренебречь, а другие считают, что необходимо уточнить теорию удара Герца путём учета сил инерции, так как возникшие при соударении колебания существенно влияют на распределение местных напряжений в зоне контакта и на весь процесс соударения».

Поиски компромисса переместились в область синтеза волновой теории и теории Герца, который использовали в своих работах такие исследователи как Сирс, С.П.Тимошенко, Н.А.Кильчевский.

3.3О формулировке понятия удар

Несмотря на то, что человек практически со времени своего рождения сталкивается с явлением, которое мы называем ударом, несмотря на то, что наука уже давно занимается определением природы удара и его количественных показателей, до сих пор нет чёткой и общепризнанной формулировки этого явления. Разные авторы в зависимости от решаемых ими задач дают разные, порой исключающие друг друга, определения. Основной причиной такого положения являются попытки объяснить природу удара с разных позиций: классической механики, теории упругости, волновой теории, выводы которых не всегда совпадают. Известны теории Гюйгенса, Сен-Венана, Герца, «теории типа Герца» и так далее.

Рассмотрим несколько примеров формулировок из совремённой учебной и научно-технической литературы.

А.А.Яблонский (Курс теоретической механики, ч.2, «Высшая школа», 1962, стр.273):

«Явление, при котором за ничтожно малый промежуток времени скорости точек тела изменяются на конечную величину, называется ударом».

Л.Г.Лойцянский и А.И.Лурье (Курс теоретической механики, т.2, ГИТТЛ, 1955, стр.125):

«Если движущаяся материальная точка мгновенно изменяет свою скорость на конечную величину, то говорят, что она претерпевает удар».

И.Н.Бухгольц (Основной курс теоретической механики, т.2, «Наука», 1966):

«Сущность явления удара заключается в том, что при ударе происходит конечное изменение скорости, а следовательно, и количества движения за весьма малый промежуток времени, практически измеряемый тысячными и меньшими долями секунды».

А.А.Кобринский и А.Е.Кобринский (Двумерные виброударные системы. «Наука», М., 1981):

«Ударом называют такое движение, при котором за очень малый промежуток времени (например, за интервалы порядка тысячных и десятитысячных долей секунды) скорость системы получает конечные, а не малые изменения. Соответственно этому в результате удара на конечную величину изменяется также и количество движения системы».

Я.Г.Пановко (Введение в теорию механического удара. «Наука», М., 1977, стр.10.):

«Выражения «кратковременность», «резкие изменения», «весьма малые», «весьма большие» – расплывчаты и лишены количественной четкости. Однако неясности могут быть устранены, если определить удар как совокупность явлений, связанных с резкими изменениями скоростей точек механической системы, происходящими за столь малое время, что по сравнению с импульсами возникающих при этом ударных сил можно пренебречь импульсами всех остальных сил».

Е.В.Александров и В.Б.Соколинский (Прикладная теория и расчёты ударных систем. «Наука», М., 1969, стр.7):

«Механическим ударом называется явление, возникающее при столкновении тел, сопровождающееся полным или частичным переходом кинетической энергии тел в энергию их деформации…

Момент встречи тел, движущихся до этого с различными скоростями, называют началом удара; момент, когда взаимодействие тел прекращается – концом удара. Интервал между этими двумя моментами называют временем или продолжительностью удара».

Н.А.Кильчевский (Динамическое контактное сжатие твёрдых тел. Удар. «Наукова думка», 1976):

«Условимся в дальнейшем термин «удар» распространять лишь на динамическое взаимодействие тел, массой которых нельзя пренебрегать… Одна из основных особенностей явлений, объединённых термином «удар», заключается в их быстрой изменяемости во времени. Вообще следует различать геометрический контакт – касание поверхностей соударяющихся тел – и механический, сопровождающийся силовым взаимодействием тел».

Сопоставительный анализ приведенных формулировок убедительно показывает, что в теоретической механике остается белым пятном как полное понимание природы физического явления, обозначенного словом удар, так и само содержание понятия удар.

Недопустимость определения природы удара как явления с помощью количественных характеристик уже отмечена в процитированном выше определении Я.Г.Пановко.

Такие явления, как «мгновенное изменение скорости», «конечное изменение скорости», «импульсы ударных сил», «переход кинетической энергии тел в энергию их деформации» и ряд других, характеризуют либо отдельные этапы в цепи событий, либо последствие события. Ни одно из них не располагает приоритетом в характеристике явления в целом.

Очевидно, было бы логичным рассматривать как единый событийный сюжет все переходные процессы, связанные с соударением: от одного стационарного состояния тел до последующего. И весь этот физический процесс рассматривать как соударение.

Е.В.Александров и В.Б.Соколинский в цитируемом выше источнике предлагают считать момент, когда взаимодействие тел прекращается, концом удара. Под взаимодействием понимают процесс перехода энергии деформации сжатия через контактную площадку (Глава5. «Формирование и распространение продольных волн»). Но, если удар заканчивается деформацией контактной площадки, тогда что же такое всё остальное? Известно, что тела в результате соударения разгоняются в обратном направлении, вибрируют и нагреваются. Спрашивается, входят ли потери на тепло и вибрацию в энергетический баланс удара или это издержки процессов за пределами удара?

Выраженное в формуле Кильчевского разграничение понятий геометрического контакта соударяющихся тел (то есть, имеющих разную скорость) и их механического контакта, сопровождающегося силовым взаимодействием, представляется сомнительным. Касание материальных поверхностей соударяющихся тел в момент перехода координаты разделяющего их пространства через нуль, неизменно вызовет силовые взаимодействия. И как бы они не были малы, будет положено начало процессу, который мы именуем ударом.

Подводя итоги натоящего обзора, мы вынуждены признать, что попытки втиснуть в единую научную формулировку всех физических показателей соударения под именем удар оказались стилистически неподъёмной задачей. Это естественно, постольку, поскольку мы имеем дело с многофакторным процессом, каждая фаза которого имеет свою закономерность.

3.4Нагружение и свойства материалов

Для наглядного представления процессов распространения единичного импульса напряжения в твёрдом упругом теле, а также волны напряжения при контактном взаимодействии тел, необходимо построить динамическую модель этих тел. Имея в виду то обстоятельство, что в процессе передачи импульса напряжения отдельные участки тела претерпевают самостоятельные эволюции во времени, удобно динамическую модель представить в виде тела с распределёнными параметрами. А возникающие по мере развития процесса соударения смещения, деформации и структурные изменения рассматривать, как уже присутствующие в данный момент времени в данных координатах.

Вариант такой модели представлен на рисунке 3.1. Рассматривается соударение движущегося со скоростью V₁ тела m₁ с неподвижным телом m₂. Ненагруженное тело представляется в виде пакета плоских элементов, обладающих элементарной размерностью и массой, связанных между собой невесомыми звеньями упругости. Памятуя об электрическом (полевом) происхождении упругости, будем считать такую абстракцию допустимой. Предполагается, что в результате смещения названные элементы (звенья) способны изменять свои размеры. При этом у первого изменяется плотность, а у второго – потенциал(упругость).

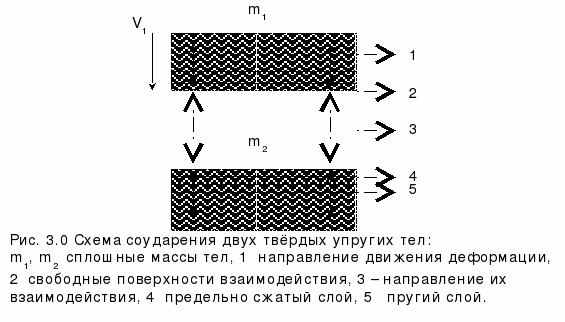
Как это видно на рисунке, в момент возникновения динамического контакта незначительные неровности (выступы и впадины) сминаются за счет движения тел, и во взаимодействие вступают две плоскости, на фронте которых равномерно распределены односторонне свободные от связей молекулы вещества рассматриваемых тел. Возникшие на молекулярном уровне мощные силы отталкивания понуждают тонкий граничный слой сдвигаться в теле1 и в теле 2, как это показано на рисунке. При этом скорость смещения слоя относительно тела ударника изменяется за время dt , величина которого стремится к нулю, а ускорение a за это же время, соответственно, стремится к бесконечности.

Смещение граничного слоя в материальном пространстве тел ударника и наковальни вызывает деформацию близлежащих слоёв в пределах их упругости и одновремённое их смещение в целом в направлении динамического действия. Это выглядит так, как если бы свободная пружина сжималась и одновремённо смещалась в пространстве. В результате смещения сечений и сжатия объёма возникают напряжения, которые, в свою очередь, формируют силы реакции. Эти силы имеют статическую природу и не изменяют своей величины, пока остаётся неизменной возникшая деформация. По мере возрастания подвергнутого сжатию объёма, растёт и величина сил реакции. При этом силы реакции, направленные в сторону площадки динамического контакта, вызывают предельное сжатие и обеспечивают на время своего действия удержание на связи ударник и наковальню, временно представляющих единое целое.

Противостоящие площадке контакта концы образовавшейся в теле соударяющихся тел пружины стремятся распрямиться и таким образом формируют зону сжатия, которая в виде волны деформации устремляется в сторону свободного от связей в направлении реакции торца. Волна деформации отражается от поверхности свободного торца и формирует ускорение тела в обратном направлении. Более подробно этот процесс будет рассмотрен в последующих разделах на примере соударения тел типа стержней.

Образовавшийся крутой фронт перемещения микрообъёмов вещества в зоне контакта, характеризуется чрезвычайно высокими показателями ускорения и силового воздействия на близлежащие плоские объёмы. Можно предположить, что в результате резкого изменения межмолекулярных расстояний в плоскости силового воздействия, вещество приобретает свойство жидкости. Или, по крайней мере, состояние, которое характеризуется незжимаемостью и текучестью. Это предположение вполне соответствует совремённым представлениям о процессах, сопровождающих удар.

А.Н.Динник (9) определил с помощью вычислений на основе теории Герца, что при соударении упругих тел, возникают напряжения, измеряющиеся десятками тысяч кг/см². При скорости сближения стальных шаров, равной 1см/сек, в центре области сжатия возникает нормальное напряжение σ_z = 7459кг\см²; при скорости 100см\сек возникает напряжение σ_z = 50480кг/см².

Н.А.Кильчевский (23) отмечает (имея ввиду, что другие главные напряжения связаны соотношением σ_x = σ_y = 0,8σ_z), что эллипсоид напряжений в этом случае приближается к шару, то есть эллипсоиду напряжений в маловязкой жидкости.

Ссылаясь на выводы Бриджмена, Кольский (8) отмечает, что сжимаемость твёрдых тел возрастает при высоких давлениях. Анализируя условия возникновения ударных волн в цилиндрическом стержне, он показал, что при возрастании давления за пределом текучести на сдвиг материал ведёт себя подобно жидкости. Толщина переходной зоны между фронтом ударной волны и невозмущенным материалом зависит от свойств среды и управляется диссипативными силами, влияние которых становится существенным при возрастании перепада скорости в переходной зоне. Для жидкостей показано, что эта толщина имеет порядок одного среднего свободного пробега молекулы.

Рассматривая процесс соударения тел на примере гидродинамической модели, А.А.Дерибас (9) показал, что для определения неизвестных параметров, характеризующих движение тел после удара и изменение формы ударяющего тела при переходе его поверхностных слоёв из твёрдого состояния в жидкое, применяется принцип наименьшего принуждения (принцип Гаусса).

Изменение агрегатного состояния твёрдого вещества замечено при силовых процессах ковки, прокатки и волочения металлов.

В результате проведенных в последнее время исследований (39) обнаружен феномен сверхпластичности металлических тел и сплавов при их нагружении и деформациях растяжения.

А.А.Пресняков (39) приходит к выводу о том, что этот феномен является показателем совершенно нового состояния вещества в процессе деформации.

«Это состояние металлического вещества характеризуетс, прежде всего, интенсивным распадом кристаллической решётки одной фазы и процессами образования новых фаз. Главной особенностью этого состояния является деформирование, препятствующее завершению превращения и сохраняющее вещество в состоянии очень высокой подвижности, не достижимой в обычных условиях. Другими словами, интенсивный распад решётки метастабильных фаз в процессе деформации приводит атомы тела в состояние исключительной подвижности, никогда не обнаруживающейся в обычных условиях. В этом случае атомы компонентов могут мигрировать на очень большие расстояния, сравнимые с макроскопическими размерами деформируемого тела, не вступая между собой во взаимодействие, необходимое для формирования новой решётки. Возникновению новой фазы препятствуют очень высокие скорости перемещения атомов, вследствие чего время нахождения атомов компонентов в контакте недостаточно для установления связей между ними. Появляется новая метастабильная промежуточная фаза, характеризующаяся очень малыми силами связи между атомами, своеобразная «квази-жидкость».

Изложенные обстоятельсва непременно должны учитываться при построении динамических моделей как единичных силовых возмущений в упругой среде, так и соударений упругих тел в целом.

3.5Распространённые теории соударений

В научной, технической и учебной литературе присутствует целый ряд принципиально отличных трактовок природы удара и связанных с ним механических процессов типа соударения упругих тел, их динамического нагружения, вибрации и тому подобного. При научной интепретации таких явлений, как разгон, ускорение, равномерное движение и инерция реального тела, наиболее рельефно выступают противоречия, присущие основным законам механики.

В ракурсе проводимого нами анализа читателю предоставляется возможность ознакомиться с некоторыми наиболее характерными противоречиями в работах таких авторитетных исследователей, как Г.Кольский (Осксфорд), Р.Фейнман (Калифорнийский Технологический институт), Е.В.Александров и В.Б.Соколинский (Институт горного дела имени Скочинского).

Г.Кольский. Волны напряжения в твёрдых телах. ИЛ, М., 1955. Стр.7-8 и 50-52.

«В динамике твёрдого тела предполагается, что напряжения, возникающие при приложении силы в некоторой точке тела, мгновенно приводят в движение каждую его другую точку, так что можно считать, что сила вызывает линейное ускорение всего тела как целого и угловое ускорение его относительно центра тяжести.

С другой стороны, в теории упругости тело рассматривается как находящееся в равновесии под действием приложенных сил, причём предполагается, что упругие деформации уже приняли их статическое значение. Такая трактовка достаточно точна для задач, в которых время между моментом приложения нагрузки и установлением действительного равновесия мало по сравнению с промежутками времени, в течение которых производятся наблюдения. Однако когда мы исследуем действие сил, приложенных лишь на короткий промежуток времени или быстро изменяющихся, это явление надо рассматривать с точки зрения распространения волн напряжения.

К
онечность скорости волн в жидкой среде с плотностью ρ и модулем всестороннего сжатия κ можно вывести непосредственно из уравнения движения такой среды. Эта скорость распространения равна

В
безграничных изотропных твёрдых телах могут распространяться два типа упругих волн: волны расширения со скоростью

где -- модуль сдвига, и волны искажения, скорость распространения которой равна ()¹² .»

После изложения основных положений теории распространения волн напряжения в ограниченной упругой среде Кольский приводит пример механических эволюций упругого стержня после приложения нагрузки. Рассмотрим этот сюжет в редакции автора.

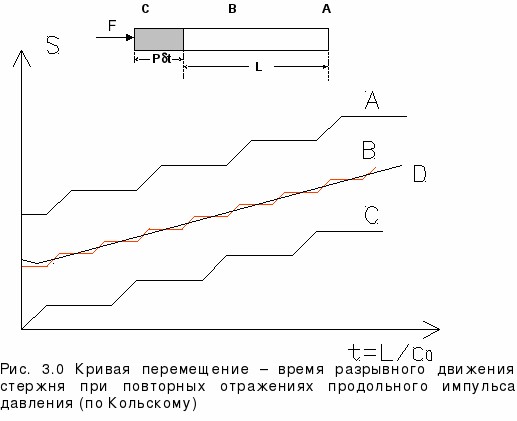
«В качестве иллюстрации результатов элементарного подхода рассмотрим движение свободно подвешенного стержня АС (рис. 3.2), к концу С которого в течение короткого промежутка времени t приложена постоянная сила Р.»

Кривые относятся к движению: А – переднего торца стержня; В – средней точки стержня; С – противоположного торца стержня и D – центра тяжести стержня. Для наглядности перемещения сильно увеличены по сравнению с длиной стержня.

«

Общее количество движения, сообщаемое стержню, равно P t , и, если масса стержня равна M, то центр тяжести должен двигаться с постоянной скоростью V, такой, что MV = P t. В момент снятия силы часть стержня длины с₀ t находится в состоянии сжатия, а остальная часть находится в состоянии покоя и не деформирована. Импульс напряжения сохраняет постоянную длину и распространяется вдоль стержня с постоянной скоростью c₀. Как видно из уравнения (выведенного ранее, авт.), скорость частицы, производимая импульсом, равна

и масса, движущаяся с этой скоростью, равна Ac₀ t, так что количество движения по-прежнему равно P t (здесь - плотность стержня; с₀ – скорость звука для данной среды; А – площадь сечения стержня).

Когда импульс достигает свободного конца А стержня, он отражается как импульс растяжения, распространяющийся в обратном направлении со скоростью c₀. Этот импульс растяжения отражается от другого конца стержня как импульс сжатия, и повторяется полный цикл.

Импульс пробегает длину стержня L за время Lc₀ (на рисунке показано движение при t < 2Lc₀). A и C – кривые перемещение-время концов стержня, движущихся рывками через интервалы 2Lc₀ ; B – такая же кривая для средней точки стержня, которая приходит в движение вдвое чаще, так как импульс проходит через неё дважды при отражении от каждого конца ; D – кривая для центра тяжести стержня, представляющая параболу для промежутка времени t, в течение которого приложена постоянная сила P, после чего она представляет прямую линию.

Необходимость постоянной с»корости центра тяжести после того, как сила снята, связана с различием между массой единицы длины в невозмущенной области стержня и на длине с₀t, содержащей импульс. Поэтому как движущийся вперёд импульс сжатия, так и движущийся в обратном направлении импульс растяжения приводят к движению вперёд центра тяжести. Из кривых В и D можно видеть, что для каждого цикла продолжительностью 2Lc₀ средняя точка стержня и его центр тяжести совпадают четыре раза. Два раза это происходит при прохождении через центр тяжести стержня, когда область повышенной линейной плотности симметрична относительно центра. Два других соответствуют моментам, когда половина импульса отразилась от концевого сечения. Напряжения, производимые падающей и отраженной половинами импульса, в этот момент в точности погашаются, и плотность становится равномерной по всему стержню.

В действительности длина импульса по мере распространения постепенно возрастает. Это происходит вследствие дисперсии, связанной с радиальным движением стержня, а также с внутренним трением. Ступени, показанные на рис.3.2, вследствие дисперсии становятся сглаженными, а длина импульса, в конце концов, возрастает до длины стержня. Задачу после этого можно рассматривать так, как если бы центр тяжести стержня двигался с постоянной скоростью, а стержень совершал в то же время свободные продольные колебания около этого центра. Эти колебания постепенно затухают, и остаётся только поступательное движение вперёд, которое рассматривается в динамике твёрдого тела».

Вопросы по существу заключений Г.Кольского.

1. Если скорости передачи динамических воздействий через разные среды имеют конечные и экспериментально определённые значения (сталь – 5100мсек, резина – 16мсек), то какой механизм обеспечивает мгновенную передачу энергии движения от точки к точке?

2. Если теория упругости рассматривает тело «как находящееся в равновесии под действием приложенных сил», тогда в чём состоит разница между статическим и динамическим нагружением?

3. Как следует понимать «действие сил, приложенных на короткий промежуток времени или быстро изменяющихся»?

4. Что же является причиной и что следствием в ряду физических состояний: сила, напряжение, деформация?

5. Может ли принципиально оставаться постоянной приложенная сила даже за очень короткий промежуток времени при реальном динамическом взаимодействии физических тел? Как быть с классическим определением силы как величины, численно равной изменению количества движения за элементарный отрезок времени?

6. Если в момент снятия силы часть стержня длиной c₀t находится в состоянии сжатия, а остальная часть в состоянии покоя и не деформирована, то имеем ли мы основание считать, что стержень начал своё движение? Частичная деформация стержня говорит лишь о том, что в движение пришло только ограниченное количество материальных точек, составляющих тело. А по основному определению динамики тело может начать движение в пространстве только тогда, когда все составляющие его материальные точки приобретут одинаковую по величине и направлению скорость. Как в этом случае быть с фундаментальным положением механики о том, что любая механическая система (и тело – система) не может изменить свой импульс только за счет внутренних эволюций?

7. В момент «снятия силы» ранее сжатый торцовый объём по закону Гука для упругого тела и в соответствии с требованиями симметрии должен претерпевать фазу восстановления формы. В результате возникших силовых воздействий левая часть объёма должна получить отрицательное ускорение и начать движение, противоположное приложенному импульсу силы Pt. Можно ли в этой ситуации полагать, что общее количество движения, сообщенное стержню, будет сохранять величину Pt? И можно ли принять на веру утверждение, что «если масса стержня равна М, то центр тяжести должен двигаться с постоянной скоростью V, такой, что MV = Pt?»

8. Как в свете предыдущего вопроса «импульс напряжения сохраняет постоянную длину»?

9. Можно ли считать фазу разгрузки от сжатия деформацией растяжения или это самостоятельная фаза восстановления формы?

10. «Когда импульс (чего? авт.) достигает свободного конца А стержня, он отражается как импульс напряжения, распространяющийся в обратном направлении со скоростью с₀. Этот импульс растяжения отражается от другого конца стержня как импульс сжатия, и повторяется полный цикл». Сколько же будет «повторяться» этот полный цикл? И когда, за счет чего, в каких координатах тела реализуется преобразование энергии деформации Pt в количество свободного движения тела MV?

11. За счет чего в недеформированной части «импульс напряжения сохраняет постоянную длину и распространяется вдоль стержня с постоянной скоростью с₀»? Не похоже ли это на безопорное движение?

12. По общему определению напряжение есть мера внутренних сил, возникающих в деформируемом теле под влиянием внешних воздействий, то есть относится к числу так называемых удельных величин. Оно характеризует состояние единицы площади сечения и привязано к координате этой площади. Можно ли в этом плане говорить о том, что «импульс напряжения сохраняет постоянную длину»?

13. «Отраженный импульс давления имеет ту же форму, что и падающий, но противоположен по знаку, то есть импульс сжатия, отразившись, становится таким же импульсом растяжения». Как «отраженный импульс давления» может инициировать деформацию растяжения?

На рис. 3.5, иллюстрирующем разрывное движение торцов при повторных отражениях продольного импульса давления показаны рывки торцов стержня на трассе его массового разгона. Рывки приурочены к моменту времени, равному 2Lc₀, то есть к тому моменту, когда стержень предельно растянут, и все его точки приобрели новую одинаковую для всех скорость. Так не логично ли было бы говорить о рывках скорости стержня в целом? Остаётся неясным, почему в каждом последующем рывке кривая нарастания скорости не меняет угла своего наклона? Выходит, что энергия волны от рывка к рывку не расходуется. Тогда за счет чего изменяется скорость центра тяжести?

Утверждение о том, что «необходимость в постоянной скорости центра тяжести после того, как сила снята, связана с различием между массой единицы длины в невозмущенной области стержня и на длине c₀t, содержащем импульс, звучит несколько туманно.

Если предположить, что, как утверждает Кольский, длина импульса по мере распространения возрастает, тогда нужно согласится с тем, что задние сечения импульса отстают от впереди идущих в результате потери скорости. Но это не подтверждается экспериментально. Тем более это не может коррелироваться «с последствиями дисперсии, связанной с радиальным движением стержня, и внутренним трением».

Остаётся также неясным, как соотносятся несбалансированные рывки торцов стержня и последующие их гармонические колебания относительно центра тяжести стержня с частотой его собственных колебаний.

Е.В.Александров В.Б.Соколинский. Прикладная теория и расчеты ударных систем. М., «Наука», 1969. Стр. 92-95.

Свою оригинальную версию природы и основных закономерностей удара упомянутые авторы строят на позициях критического отношения к постулатам классической механики и теории упругости. Их выводы базируются на экспериментальных данных, полученных с помощью тензометрических датчиков, закреплённых на поверхностях динамически нагружаемых тел (в основном типа стержней). Рассмотрим главные из предложенных авторами формулировки и попытаемся оценить их обоснованность и достоверность.

«Причиной возникновения сил на поверхности контакта соударяющихся тел является их инерция, противодействующая любому изменению скорости тел: как ускорению, так и замедлению. Но, вступив в непосредственный контакт, имея общую контактную площадку, стержни не могут сохранять прежние скорости, и потому в результате удара контактная площадка получает некоторую среднюю скорость, которая меньше v₀₁ (массовая скорость стержня-ударника), но больше v₁₂ (скорость движущегося сечения в теле ударяемого стержня).

Возникновение силы удара на контакте стержней приводит к одновремённому появлению напряжений на торцах стержней. Согласно основному положению волновой теории удара эти напряжения распространяются от поверхности контакта по стержням со скоростью звука. Распространение представляется в виде последовательного соударения соседних сечений стержня, идентичных предшествующему соударению торцовых поверхностей. А поскольку ни сечение, ни свойства материала по длине стержня не меняются, в результате соударения в сечениях появляются те же силы и скорости, что и на торцах.

Через время dt волна скорости v , распространяющаяся по стержням со скоростями a₁ и a₂ ,охватывает объёмы в первом стержне F₁ a₁ dt и во втором F₂ a₂ dt , что соответствует массам m₁ = F_{1 1} a₁ dt и m₂=F_{2 2} a₂ dt.

В результате изменения скоростей с v₀₁ до v в первом стержне и с v₀₂ до v во втором стержне, количество движения этих масс изменится на величину

m₁(v₀₁ – v) = F_{1 1} a₁ dt(v₀₁ – v) в первом стержне,

m₂(v₀₂ - v) = F_{2 2} a₂ dt(v₀₂ – v ) во втором стержне.

Ускорение в момент плоского удара оказывается бесконечно большим, поскольку скорость сечений стержней в момент удара изменяется скачком от v₀₁ или v₀₂ до v = const за время t =0».

Вопросы по существу заключений Александрова и Соколинского.

1. Что есть инерция – дополнительное свойство тел или возникающее по воле обстоятельств физическое явление?

2. Сила по Ньютону F = mdvdt – это изменение количества движения во времени. Как инерция становится «причиной возникновения сил», если она «противодействует любому изменению скорости тел»?

3. «Контактная площадка» – это объём или плоскость в координатах тела?

4. В чём физическая причина того, что «вступив в непосредственный контакт, имея общую контактную площадку, стержни не могут сохранять прежние скорости»?

5. Если бы массовая скорость части ударника v действительно оказалась бы меньше v₀₁, то стержень должен был бы начать замедление за счет собственных ресурсов, что противоречит логике.

6. Что есть сила удара на контакте?

7. Можно ли представлять распространение напряжений вдоль стержня после соударения «в виде последовательного соударения соседних сечений стержня, идентичных соударению торцовых поверхностей», если учесть, что в промежутке между торцами было свободное пространство, а в промежутке между гипотетическими соударяющимися сечениями стержня – составляющее его вещество?

8. Можно ли допустить такую ситуацию, чтобы внутри тела перемещалась «масса m₁ объёмом F₁a₁dt со скоростью v»?

9. Если предположить, что в процессе соударения «ни сечение, ни свойства материала по длине стержня не меняются», то за счёт чего происходит передача движения, и откуда «в сечениях появляются те же силы и скорости, что и на торцах»?

10. Что имеется ввиду под выражением «момент плоского удара»? Ускорение чего «оказывается бесконечно большим»? Как соотнести эти определения с предложенной авторами формулировкой удара: «Механическим ударом называется явление, возникающее при столкновении тел, сопровождающееся полным или частичным переходом кинетической энергии тел в энергию их деформации»?

11. Почему «сила удара» появляется на контакте, а не на торцах стержней?

12. Как это может быть, чтобы «через время dt волна скорости v распространилась по стержням со скоростями a₁ и a₂» ,если заведомо известно, что скорости звука для данной среды многократно превышают по величине массовую скорость v?

Излагая теорию плоского удара в стержне (стр. 90), авторы утверждают:

«Напряжения, направленные вдоль оси стержня _x, вызывают кроме продольных U_x и поперечные деформации U_у и U_z,, вызванные пуассоновым поперечным увеличением тел под действием продольной нагрузки. Эти деформации могут быть найдены из известных в теории упругости соотношений».

Используя эти соотношения и полагая, что _у и _z равны нулю, приходят к заключению, что _x распределяется равномерно по сечению стержня, то есть, не зависит от координат у и z. Абстрагируясь от смысловой путаницы со словом «вызывают», сформулируем вопросы по существу. Если напряжения вызывают продольную деформацию, то что является первопричиной появления напряжений? Физически остаётся не ясным, поперечные деформации есть причина или следствие пуассонового поперечного увеличения тел? Что следует понимать под определением «продольная нагрузка»: сжатие торцовой части, знакопеременная волна деформаций или продольное сплошное растяжение?

В формуле сил, действующих при соударении двух стержней сечением F₁ и F₂ , плотностью ₁ и ₂ введено понятие жесткости тел С, равное произведению акустической жесткости на площадь поперечного сечения:

С₁ = F_{1 1} a₁ и C₂ = F_{2 2} a_{2 .}

В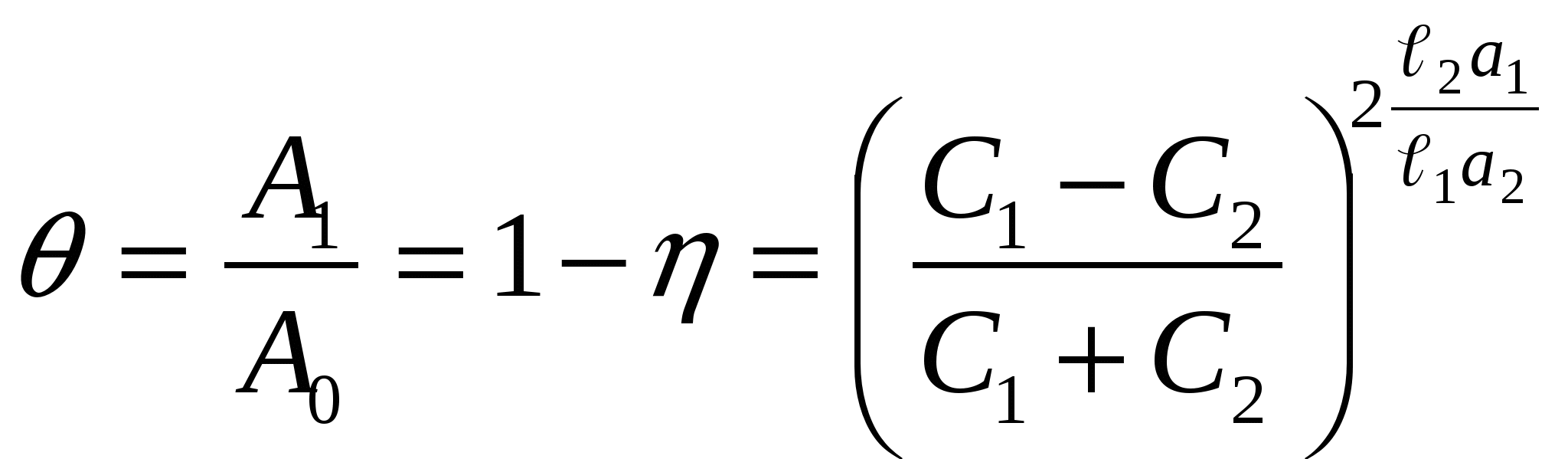
ычисленный на основании проведенного расчета «коэффициент потерь энергии при передаче удара»:

На основании этой формулы авторы приходят к выводу: «В формулу не входят непосредственно массы соударяющихся стержней, поэтому можно утверждать, что вопреки классической механике упругого удара величина переданной энергии не зависит от масс соударяющихся стержней».

Но это же противоречит основному постулату динамики: изменение движения тела в целом возможно только при условии, что все его точки (то есть, вся масса) согласованно изменят свои скорости. Ошибочность изложенного вывода легко выявляется, если в формулу вернуть введенное авторами ранее обозначение C = Fa. Тогда в определении коэффициента мы обнаружим в качестве множителей площадь сечения, длину стержня и плотность вещества, которые как раз и характеризуют массу.

Если «величина переданной энергии не зависит от масс соударяющихся стержней», то возникает закономерный вопрос, что же является носителем энергии движения, как не сама масса тел?

Здесь мы не можем не вспомнить заключение классика марксизма В.И.Ленина:

«В мире нет ничего, кроме движущейся материи, и движущаяся материя не может двигаться иначе, как в пространстве и времени» (Материализм и эмпириокритицизм. Стр171).

Но продолжим анализ рассматриваемой прикладной теории. Авторы утверждают:

«Возникающая в нагруженном конце неподвижного стержня сила N должна быть равной силе инерции ударяющего тела. Вследствие этого на тех участках стержней, до которых успело распространиться действие силы, неизбежны деформации».

Как может возникнуть в локально нагруженном конце неподвижного стержня сжимающая сила N, равная силе инерции всего ударяющего тела? Почему она должна быть равной силе инерции всего ударяющего тела, в то время как большая часть его массы за пределами торцовой деформации не претерпевает никаких изменений? Как соотносятся понятия инерция и сила инерции; сила и действие силы? Посредством чего «успело распространиться действие силы до участков, где неизбежны деформации»?

«Итак, при формировании волн напряжения, являющихся следствием абсолютно упругого удара, всегда происходит разделение энергии удара на кинетическую и потенциальную формы».

В приведенной выше формулировке явления удар утверждалось о переходе кинетической энергии тел в энергию их деформации. Можно ли считать разделение и переход (превращение) энергии адекватными понятиями?

«В приведенных примерах (соударения стержней, авт.) рассматривается распределение сообщенной стержням энергии и количества движения. Перенос энергии волны тесно связан с наличием в волне двух форм энергии: потенциальной и кинетической. Напряжённые слои стержня, перемещаясь, совершают работу, которая превращается в энергию упругой деформации и кинетическую энергию частиц соседнего слоя. Каждый напряжённый участок волны ведёт себя как абсолютно твёрдое тело, которое, перемещаясь, не изменяет своих размеров и напряжения, а передаёт лишь энергию, не высвобождая и не поглощая её».

Это метафизика. Как можно передать энергию движения участком волны, который не изменяет ни своих размеров, ни напряжения? Как можно передать энергию, не высвобождая её? Согласно принятым в теоретической механике исходным положениям частицей или материальной точкой принято считать объект, лишённый протяженности. Как, по представлению авторов, «частицы соседнего слоя» могут усвоить энергию упругой деформации? Возникает также вопрос, о каком распределении количества сообщенного стержню движения идёт речь?

«Поперечными деформациями – сужением или расширением стержней можно пренебречь, так как при длине волны, значительно превосходящей диаметр стержней, они очень малы и практически не имеют никакого значения».

Известно, что наибольшее формоизменение испытывают торцевые объёмы, более того, деформация торца зависит преимущественно от скорости ударника и предшествует формированию волны деформации и сопровождающей её волны напряжений в сечениях. Деформация торцов хорошо визуально обнаруживается на побывавших в работе ударниках.

Допустимо ли, опираясь только на математическую интерпретацию продольной волны напряжений, игнорировать физические процессы, возникающие на начальном этапе соударения, и на заключительной послеударной фазе, когда стержень подвергается деформации сплошного продольного растяжения, завершая тем самым хронологический ряд преобразований продольной волны?

«Если пренебречь дисперсией, то последовательное прохождение волн сжатия и растяжения должно продолжаться до бесконечности.

Итак, при соударении короткого стержня с покоящимся длинным равного сечения, вся его кинетическая энергия передаётся длинному, который отскакивает от остающегося неподвижным (?) короткого стержня и перемещается в направлении удара; при этом по длинному попеременно в противоположные стороны пробегают волны сжатия и растяжения».

Если бы в действительности последовательное прохождение волн сжатия и растяжения продолжалось до бесконечности, то это означало бы лишь то, что энергия возмущения локализовалась в координатах ударяемого тела, и для массового ускорения его в пространстве не осталось бы причины. Если же после отхода ударяемого тела, в нём все-таки пробегают волны сжатия-растяжения, то это указывает на то, что часть энергии, полученной от ударника, преобразуется в тепло. И теперь уже нельзя утверждать, что вся кинетическая энергия короткого стержня передаётся длинному: часть её уходит на издержки трансформации движения.

Суммируя все изложенные вопросы, мы можем сформулировать один заключительный генеральный вопрос: где скрыта ошибка в изложении природы ударных взаимодействий?

Р.Фейнман. Фейнмановские лекции по физике. М., изд. «Мир», стр. 190.

C точки зрения критического исследования получивших признание трактовок динамики удара большой интерес представляют оригинальные идеи по этому поводу, которые доктор Фейнман изложил в своей лекции перед слушателями Калифорнийского Технологического института. В приведенном ниже фрагменте сохранен несколько свободный стиль живой беседы автора.

«Существует множество примеров соударений, в которых тела не сцепляются, как, например, столкновение двух тел равной массы и одинаковой скорости, которые затем разлетаются в разные стороны. На какой-то краткий миг они соприкасаются и сжимаются. В момент наибольшего сжатия они останавливаются и их кинетическая энергия полностью переходит в энергию упругого сжатия ( они как две сжатые пружины).

Эта энергия определяется из кинетической энергии, которой обладали тела до столкновения и которая равна нулю в момент их остановки. Однако кинетическая энергия теряется только на одно мгновение. Сжатое состояние, в котором находятся наши тела, -- это всё равно, что заряд в предыдущих примерах, который при взрыве выделяет энергию. В следующее мгновение происходит нечто, подобное взрыву – тела разжимаются, отталкиваются друг от друга и разлетаются в разные стороны. Эта часть процесса тоже хорошо знакома: тела полетят в разные стороны с одинаковыми скоростями. Однако скорости отдачи, вообще говоря, будут меньше тех начальных скоростей, при которых они столкнулись, ибо для взрыва используется не вся энергия, а только какая-то её часть, но это уже зависит от свойств материала, из которого сделаны тела. Если это мягкий материал, то кинетическая энергия почти не выделяется, но если это что-то более упругое, то тела более охотно отскакивают друг от друга.

Неиспользованный остаток энергии превращается в тепло и вибрацию, тела нагреваются и дрожат; впрочем, энергия вибрации тоже вскоре превращается в тепло. В принципе можно сделать тела из столь упругого материала, что на тепло и вибрацию не будет расходоваться никакой энергии, а скорости разлёта в этом случае будут практически равными начальным. Такое соударение мы называем упругим.

Тот факт, что скорости до и после соударения равны, – заслуга не закона сохранения импульса, а закона сохранения энергии, но то, что скорости разлёта равны друг другу, в этом уже повинен закон сохранения импульса.

Давайте разберём интересный пример упругого столкновения двух тел равных масс. Если такие тела ударяются друг о друга с какою-то равной скоростью, то по соображениям симметрии они должны разлететься в стороны с той же скоростью».

При солидарности с доктором Фейнманом в объяснении механизма соударения, которое не совпадает с трактовками классической механики, волновой и прикладной теориями удара, мы не можем также избежать ряда вопросов принципиального характера.

1. Какова теоретически предполагаемая размерность «краткого мига», на который тела соприкасаются и сжимаются?

2. Если допустить возможность полного перехода кинетической энергии в энергию упругого сжатия, то не означает ли это существование механизма, коэффициент полезного действия которого равен единице?

3. Если «кинетическая энергия теряется только на одно мгновение», то что же происходит в пределах этого мгновения, когда известно, что энергия принципиально не исчезает и не появляется вновь?

4. Тела «разжимаются» и «отталкиваются друг от друга» – это что с физической точки зрения?

5. Если всё же допустить, что тела «отталкиваются» друг от друга как две соприкасающиеся торцами сжатые пружины, то в момент, когда они отойдут друг от друга, в кинетическую форму перейдет только половина потенциальной энергии сжатия, и скорости их приобретут только половинные значения от исходных. А как быть со второй половиной?

6. Из приведенных объяснений можно сделать вывод, что волновые процессы, сопровождающие «нечто подобное взрыву», на обмен скоростями не влияют?

7. При наличии упругости «тела более охотно» отскакивают друг от друга. В каком смысле: раньше, быстрее или дальше?

8. Откуда взялся «неиспользованный остаток энергии»? Можно ли считать, что он «зависит от свойств материала»?

9. Через какой механизм энергия возвратно-поступательного движения (вибрации) превращается в тепло?

10. Можно ли считать соударение упругим только при условии равенства скоростей разлёта?

11. Если допустить, что «скорости до и после соударения равны», то это будет означать, что мы имеем дело с механической системой, к.п.д. которой равен единице. Раз это не возможно, то и постановка вопроса о законе сохранения энергии в кинетическом измерении становится проблемной. То же можно сказать и о законе сохранения импульса.

Глава 4
Пространственно – временная модель соударений

Опираясь на изложенную концепцию движения как физического процесса, исполняемого отдельно взятым свободным телом в окружающем его пространстве, построим хронологический ряд эволюций тела в пространстве и сопутствующие ему формоизменения в его собственных координатах (деформации и преобразования форм механической энергии). Рассмотрим в пространстве и времени последовательность событий, сопровождающих процесс взаимодействия тел при столкновении, и сформулируем конечный результат этого процесса. В результате получим пространственно – временную схему взаимодействия или, другими словами, пространственно – временную модель соударения.

4.1Соударение с равными скоростями тел

Эта схема представлена на рисунке 4.1 применительно к двум соударяющемся стержням одинаковых размеров, массы и материала, движущимся навстречу друг другу вдоль общей оси с равными и противоположно направленными скоростями. Предполагается, что рассматриваемые стержни вполне упруги, то есть обладают способностью сокращаться при приложении нагрузки и восстанавливать свою форму при её снятии.

Принятие таких идеализированных и упрощенных условий позволит легче выявить основные закономерности процесса и затем распространить их на более сложные случаи по конфигурации, массе, упругости, пластичности и так далее.

Имеется в виду, что торцевые сечения стержней строго перпендикулярны их осям и имеют минимальную шероховатость поверхности; плотность и упругость материала равномерно распределены по длине стержней.

Так как начальные скорости V_A0 и V_B0 известны, то собственное движение тел в пространстве будет отражать система координат XY, одновременно привязанная к обоим телам и для упрощения рассматривающая тела в плоском изображении. Для изучения внутренних механических процессов, которые локализованы в координатах тела и не влияют на изменение положения тела в пространстве, воспользуемся частными координатами X'Y' и X˝Y˝. К таким процессам относятся смещения граничных поверхностей, местные статические и динамические деформации, волны деформации, а также деформации тел в целом. Принципиально каждая из систем координат живет по своему времени. Но для сопоставления того, что происходит «в то время как» удобно отсчет времени вести от общей, привязанной к системам шкалы отсчета T.

Для уяснения причинно – следственной связи протекающих в пространстве и времени событий, процессов и явлений важно правильно выбрать начальные условия и пройти через все без исключения промежуточные ступени. При рассмотрении этапов соударения за основу примем динамическую модель твердого тела с распределенными параметрами, представленную на рисунке 3.1 третьей главы.

Наблюдая картину столкновения упругих тел, мы приходим к заключению, что в результате тела отталкиваются друг от друга, то есть каждое является для другого непреодолимым препятствием.

Исходя из принципиального определения движения твердого тела как согласованного марша всех составляющих его точек, мы должны признать, что движения сечений или отдельных участков тела, вызванных деформацией или порожденных последней, являются внутренними по отношению к телу в целом и влиять на скорость движения тела в пространстве не могут. Поэтому было бы не верным считать, например, смещение торцового объёма в начале взаимодействия за начало движения в обратном направлении центра тяжести тела или всего тела в целом. Было бы не верным также соотносить скорости отдельных участков со скоростью тела в целом. С другой стороны, независимо от того, с какими скоростями движутся тела до столкновения, с точки зрения начала деформации торцовая поверхность одного тела по отношению к другому всегда характеризуется скоростью, равной нулю. А деформация тела В всегда будет определяться собственной скоростью тела А независимо от собственной скорости тела В.

При вторжении тела А торцом с идеальной плоскостью в материальное пространство тела В, элементарное граничное сечение последнего за бесконечно малое время dt получает ускорение, величина которого стремится к бесконечности. С этого начинается соударение. Все действия в непосредственном сопряжении вызывают ответную реакцию, сдвинутую по фазе на 180 градусов. Наглядно последовательность всех действий можно представить в виде следующей схемы:

Внешнее движение внутреннее движение смещение сечения деформация объёма напряжение реактивные силы

внешнее реактивное движение.

На основе принятых определений рассмотрим случай соударения в свободном пространстве двух идентичных стержней, движущихся навстречу друг другу по общей оси с равными и противоположно направленными скоростями. Характерные фазы движений и состояний отображены на рисунке 4.1. Для наглядности некоторые движения и состояния, развивающиеся в одно и то же время, выделены как независимо существующие.

В словесной интерпретации изображенный графически на рис. 4.1 хронологический отчет можно изложить следующим образом:

Время t₀. Тела движутся равномерно и прямолинейно с равными и противоположно направленными скоростями к плоскости их встречи с координатой X= 0. Начальная протяженность тел соответственно L_A0 и L_B0. Все материальные точки в составе тела А и тела В имеют одинаковые согласованные скорости, равные и разнонаправленные соответственно начальным скоростям тел V_A0 и V_B0. Внутренние связи тел уравновешены и динамически сбалансированы.

Время t₁. Тела сблизились и вступили в физический контакт (механическую связь). Выступы и неровности, подверженные бесконечно большому ускорению, сминаются и заполняют микро впадины, формируя, таким образом, нивелированную площадку контакта. Две соединившиеся части, удерживаемые динамической связью, образовали временно существующее единое тело, внутри которого развивается очаг возмущения. Состояние единого целого будет теперь определяться временем, в течение которого тела будут сохранять свою изначальную скорость движения в пространстве. Или, как принято говорить, в течение времени соударения.

Время t₂. Интенсивное сжатие вещества в зоне контакта проходит участок пропорциональности упругой деформации, переходит на нелинейную часть характеристики и, наконец, достигает уровня предельного сжатия для данных параметров соударения. В зависимости от характеристик материала стержней и достаточной скорости сближения, наступает состояние, когда материал приобретает свойство квазижидкости, которая характеризуется подвижностью и несжимаемостью. В результате возникшего в промежутке гидростатического давления, возникают поперечные силы и напряжения, обеспечивающие возможность выдавливания части материала наружу и снижению противодействия проникновению стержней в пространство друг друга. Стержни несколько укорачиваются, их недеформированные части продолжают движение с изначальными скоростями. Эффект расплющивания и выдавливания хорошо просматривается на головках молотков, ударников и подобных им ударных инструментах. Формирование головной части ударяемого тела можно проследить практически при сбрасывании цилиндра из пластического материала на массивную плиту.

Поперечная деформация достигает своего критического уровня, поперечное расширение приконтактного объёма сменяется сжатием, гидростатическое давление ступенчато возрастает, отодвигая влево и вправо границу нулевой скорости.

Время t_3. Под воздействием поперечной реакции и давлением со стороны невозмущенных еще фронтальных сечений продолжающих свое движение стержней, критическое сжатие сохраняется на все время взаимодействия. Встречая на своем пути непреодолимую границу нулевой скорости, граничный объём торца непрерывно объёмно деформируется (квантуется), как показано на рисунке. В результате через некоторое время все тело стержня испытывает деформацию, напоминающую гофр. Такого типа деформации обеспечивает равномерное распределение напряжений между сечениями на всей длине стержня. Фронт волны объёмной деформации распространяется по телу со скоростью звука для данной среды. Прохождения волны объёмной деформации сопровождается волной поперечной (поверхностной) деформации, следующей за основной волной. По мере распространения волны деформации длина невозмущенной части стержня, движущейся с начальной скоростью в пространстве, монотонно убывает.

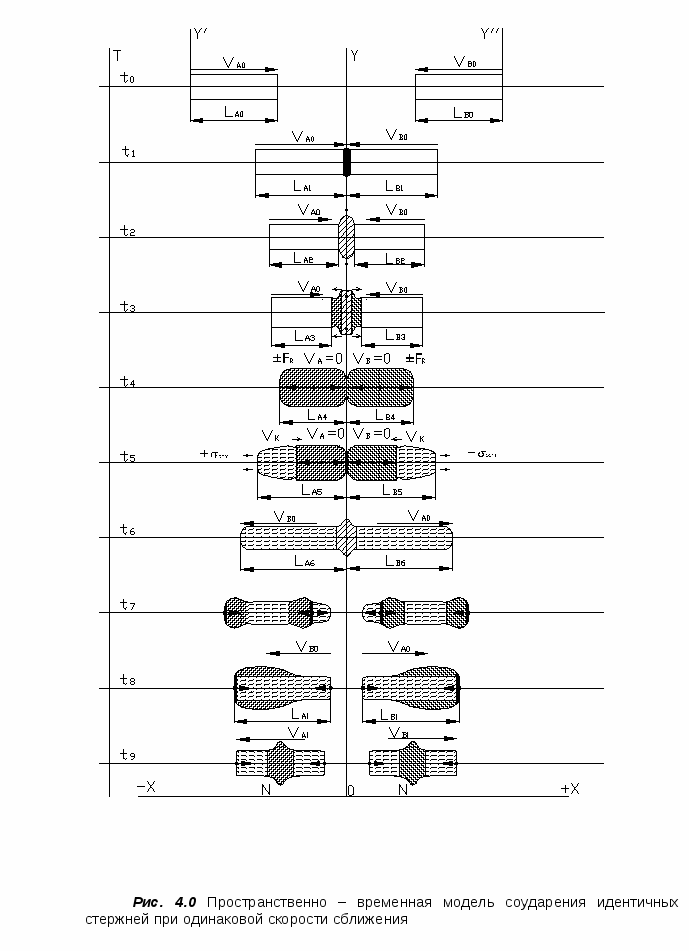
Образовавшуюся в результате движения стержней область возмущения в торцевой части можно рассматривать как пружину, которая непрерывно поджимается слева и непрерывно разжимается на своем свободном конце справа. При этом давление справа (конец пружины) распространяется в теле стержня в соответствии со скоростью звука, характерной для плотности ненагруженного вещества тела. Давление слева (начало пружины) передается через уже претерпевшую сжатие переходную зону, поэтому скорость передачи воздействия здесь определяется скоростью звука, характерной для предварительно сжатого вещества, то есть более высокой по сравнению с первой. В результате в теле пружины в течение времени взаимодействия будет поддерживаться статическая деформация, пропорциональная скорости ударника, а сама пружина будет смещаться в сторону деформации со скоростью ударника.

Время t₄. Сплошная деформация сжатия распространилась на весь объём взаимодействующих тел. Скорости их движения в пространстве приобрели нулевые значения. Вся кинетическая энергия трансформировалась в потенциальную энергию упругой деформации. Стержни превратились в статически сжатые пружины, торцами присоединенные друг к другу. В соответствии с требованиями симметрии внутри объёмов стержней возникли противоположно направленные статические силы реакции F_R. Величина этих сил легко может быть определена с помощью формул обобщенного закона деформации Гука.

Время t₅. Сжатые пружины свободно разжимаются. В целом тела сохраняют нулевые скорости движения в пространстве. В области контакта под воздействием сил реакции организуется сжатие объёма. Cо стороны свободных торцов в результате воздействия реактивных сил организуется движение поверхностных сечений, которое постепенно и равномерно распространяется на остальные, находящиеся на связи сечения. В результате в обратном направлении начинает движение волна объёмной разгрузки (восстановления формы). Как принято говорить в теории удара, отражаясь от свободной границы, волна сжатия преобразуется в такую же волну растяжения, распространяющуюся в обратном направлении с той же скоростью.

Время t_6. Волна растяжения распространилась на всю длину стержней и, пройдя через область сжатия у контакта, достигла границы раздела. В результате все точки стержней получили согласованное движение с некоторой новой скоростью V_A1 и V_B1. Продольные размеры стержней соответственно увеличились. Стержни начинают отход друг от друга, сохраняя на бывших в контакте торцах остаточную деформацию сжатия. В соответствии с требованиями симметрии половина заключенной в соединенных телах энергии приняла кинетическую форму, и вторая половина сохранила потенциальную форму. По величине приобретенные скорости равны половине их конечного значения в конце разгона: V_A1 = V_B1 = 12V_An.

Время t₇. Тела расходятся с приобретенной скоростью движения в пространстве, одновременно пребывая в состоянии сплошного растяжения. Кроме того, в районе, примыкающем к плоскости разрыва контакта, определенный участок сохраняет сжатие, унаследованное от предыдущего цикла. В результате начала процесса сокращения тела стержней на их торцах формируются развивающиеся навстречу друг другу волны сжатия. Мгновенно получивший свободу движения граничный объём со стороны контакта порождает растяжение, которое сейчас же трансформируется в импульс сжатия, который перемещается вдоль тела стержня в виде локального возмущения. Волны возникших возмущений свободно проходят друг через друга, не оказывая влияния на движение тела в целом в координатах пространства. При поочередных отражениях волны локального возмущения от свободных поверхностей торцов происходит суммирование однонаправленных возмущений волны сжатия с волной сокращения стержня. В результате длина импульса сжатия возрастает. И как только она становится равной длине стержня, происходит очередной скачок скорости тела в целом и соответственное уменьшение амплитуды напряжений в следующем цикле (то есть уменьшением доли потенциальной энергии). Число пробежек импульса и скачков изменения скорости свободного движения определяется параметрами соударения: начальной скоростью тел, их протяженностью, плотностью и т.д. Схематически разгон тела после соударения выглядит так:

V_р = 12V_р + 14V_р + 18V_р +

Время t₈. После очередного, последнего, скачка скорости, оставшейся в теле потенциальной энергии оказывается недостаточно для формирования локального импульса сжатия необходимой длины. Отражаясь поочередно от свободной границы, остаточный импульс сжатия отдает свою энергию в фонд сплошного растяжения и при каждом отражении скачком уменьшается по амплитуде. В результате он какое-то время способствует поддержанию деформации растяжения тела и вызывает его не сбалансированные колебания. В конечном счете, энергия остаточной части импульса рассеивается, и он затухает.

Время t₉. Продолжая двигаться равномерно и прямолинейно с усвоенным количеством движения, тело переходит в состояние гармонических колебаний относительно своего центрального сечения – колебаниям с собственной частотой. Эти колебания вызываются сдвинутыми во времени процессами сплошного сжатия и разрежения вещества стержней. Механическая энергия этих колебаний преобразуется в теплоту и пополнит реестр потерь при соударении.

4.2Соударение при разных скоростях

Рассмотрим вариант соударения двух идентичных по массе, материалу и конфигурации тел и построим пространственно – временную модель процесса. При построении модели принимаются во внимание все изложенные ранее исходные данные и аксиомы. Схема процесса представлена на рис. 4.2.

В том же порядке, как и в предыдущем примере, рассмотрим последовательность процессов и событий в пространстве и времени.

Время t_0. Стержни сближаются в пространстве с начальными скоростями V_A0 и V_B0 вдоль общей оси и приближаются к расчетной точке встречи. Пространственная система координат движения тел привязана к этой точке встречи. Координаты деформации, привязанные к движущимся телам, условно не показаны, чтобы не перегружать рисунок повторяющимися деталями. По условиям эксперимента принято, что V_A0 > V_B0.

Время t_1. Тела вступили в динамический контакт и сформировали переходную площадку контакта.

Время t_2. Встретивши преграду, торцы сжимаются в продольном направлении и объёмно деформируются в поперечном. В результате взаимодействующие тела несколько укорачиваются с фронтальной стороны, а их недеформируемые части сохраняют первоначальные скорости движения.

Время t_3. Вследствие растущего давления вещество в зоне контакта приобрело свойства пластичности и жидкотекучести. Гидростатическое давление равномерно распределилось в продольном и поперечном направлении. Там, где появляется свобода, господствует симметрия. Движение поверхности в поперечном направлении достигло предельного значения. В сжатом объёме возникли противостоящие силы реакции.

Время t_4. Под воздействием сил реакции возникло сокращение приконтактного объёма в поперечном направлении и возросло давление на граничные сечения в продольном направлении. В динамически соединенном теле возникло движение продольной объёмной деформации стержней под воздействием внутреннего относительно тела возмущения. Возвращаясь к своему изначальному состоянию, предельно сжатый участок контакта, еще некоторое время сохраняет свое динамическое равновесие под воздействием продолжающих сближение стержней в целом. Постоянно поддерживаемое статическое напряжение внутри зоны предельного сжатия вызывает равномерное движение в ненагруженной части стержней границы нулевой скорости. Встречаясь с неподвижной границей, торцевой объём стержня непрерывно поперечно деформируется, порождая волну объёмной деформации, движущуюся со скоростью звука в сторону свободной границы. Степень деформации с каждой стороны определяется движением стержня. В результате движения волны деформации возникают поверхностные волны и волны плоских напряжений, как это показано на рисунке.

Время t_5. Деформация сжатия охватила весь объём взаимодействующих тел. Укорочение тел достигло максимума. Скорость движения в пространстве достигла нулевого значения. Величина статической деформации каждого из тел находится в соответствии с соотношением пространственных скоростей, с которыми каждое тело внедрялось в пространство другого. Внутри стержней сформировались симметричные относительно их центральных сечений пары реактивных сил. Вся кинетическая энергия тел преобразовалась в потенциальную энергию их объёмного сжатия (деформации).

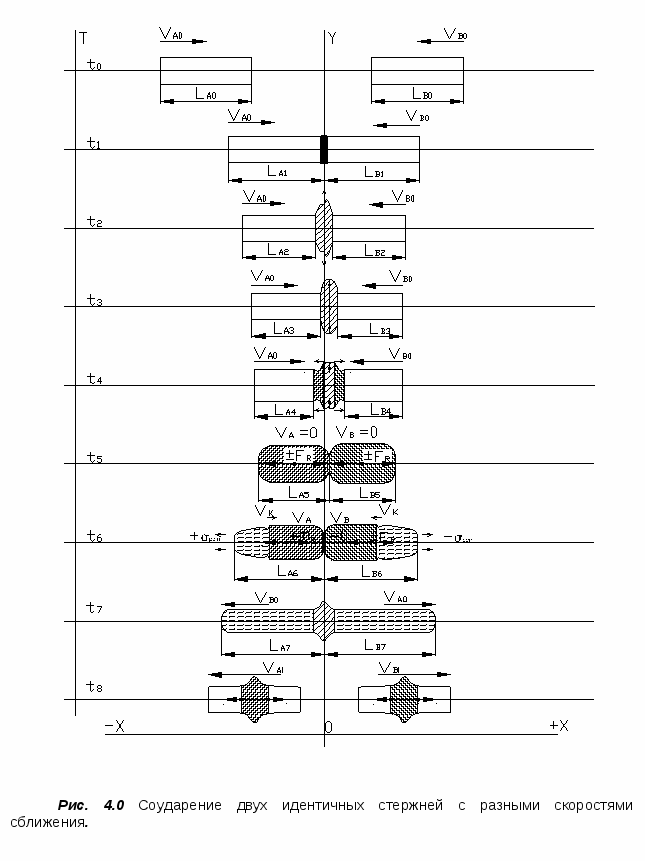
Время t_6. На свободных граничных сечениях в результате возникшего процесса разгрузки возникает свободное движение граничного сечения, которое через упругие связи увлекает в движение соседние сечения. Возникает объёмная отраженная волна растяжения, которая со скоростью падающей волны сжатия распространяется в сторону динамического контакта. В результате перераспределения напряжений в обоих сочлененных телах часть волны сжатия распространяется влево и движется в пространстве левого стержня в одном направлении с волной растяжения. Суммируясь, они обеспечат разгон стержня в обратном направлении. Одновременно развиваются с обоих торцов процессы сплошного равномерного по длине растяжения. Возникающие при этом поверхностные волны и реактивные силы показаны на схеме модели. Фактические длины стержней монотонно возрастают. Как уже отмечалось ранее, все движения частиц и участков тел являются внутренними, частными, и говорить о согласованном движении всех точек тела пока нет оснований.

Время ₇. Деформация растяжения (восстановления формы) распространилась до места раздела тел. В результате развития этой фазы механических эволюций, все точки тел приобрели одинаковые согласованные скорости, а тела в целом скачком получили новые скорости движения V_A7 и V_B7. Методика определения численного значения этих скоростей изложена в комментариях к модели на рисунке 4.1. К моменту подхода волны растяжения к области контакта, в последней организуется сжатие, обусловленное действием сил реакции. Волна растяжения свободно проходит через волну сжатия и создает предпосылку свободного отхода тел от плоскости контакта. При этом каждое тело захватывает с собой такой объём сжатия, который соответствует его скорости отхода. Далее события развиваются в соответствии со схемой рис.4.1.

Рассматривая цепь событий в целом, следует обратить внимание на один принципиальный момент: на протяжении отрезка времени вполне определенной конечной продолжительности от t₅ до t₇ тела «усваивали» передаваемую друг другу энергию и находились в состоянии нулевой скорости в пространстве.

Время t₈. Тела полностью «обменялись» скоростями, восстановили свою форму и размеры, движутся в пространстве прямолинейно и равномерно с усвоенными ими новыми скоростями –V_A и -V_B, естественно, меньшими по величине, чем начальные V_A0 и V_B0. Продолжая свое свободное движение, они еще некоторое время испытывают гармонические колебания вокруг нейтральной плоскости с частотой собственных колебаний до полного затухания последних.

Предложенный принцип построения пространственно – временной модели соударения легко может быть распространен на другие возможные варианты соударений: движущегося тела с неподвижным, тел разной протяженности и конфигурации, сплошных и полых тел, группы контактирующих тел и т.д.

На рисунке 4.3 приведен вариант соударения движущегося тела с неподвижным. Как и на предыдущих схемах, тела идентичны. Но место предполагаемой встречи теперь совпадает с плоскостью торца неподвижного тела. А, значит, и пространственная система координат теперь оказывается привязанной к неподвижному телу.

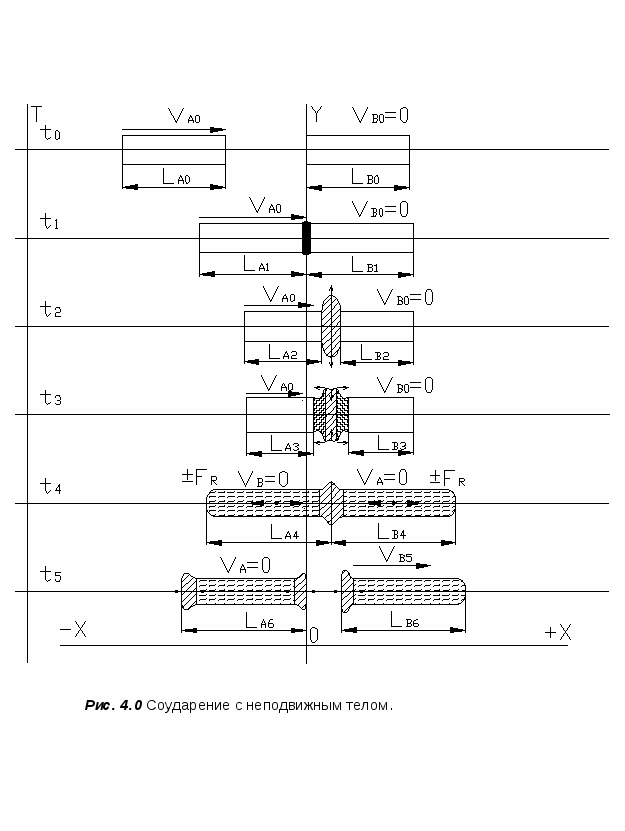
Тела сближаются, формируют площадку динамического контакта. Получая ускорение, граница неподвижного тела отодвигается, освобождая путь для внедрения движущегося тела в пространство неподвижного. Этот процесс продолжается до тех пор, пока не возникнет эффект предельного сжатия, величина которого определяется скоростью ударника и механическими свойствами охваченной движением массы вещества ударяемого тела. Благодаря возникшей динамической связи взаимодействующие тела образовали единую систему: телоА упруго-сжатый элемент телоВ. Сжатая в теле пружина, разжимаясь и сдвигая неподвижные ранее сечения, порождает волну деформации вещества стержней, как движущегося, так и неподвижного. Как было показано ранее, возникают силы реакции, продольные и поперечные волны. В течение всего времени взаимодействия возникшая «пружина» сохраняет динамическое равновесие, разряжаясь в массу тел и одновременно подзаряжаясь за счет смещения границы ударника. Как это видно на рисунке, в случае соударения с неподвижным телом очаг предельного сжатия дислоцируется в пространстве неподвижного тела. Волны сжатия отражаются от свободных поверхностей, преобразуются в волны сплошного растяжения, обеспечивая остановку ударника и разгон ударяемого тела, как это показано на рисунке 4.3 и изложено в комментариях к рисункам 4.1 и 4.2. Ударяемое тело, с опережением получившее деформацию сплошного растяжения, совершает первый рывок скорости и отходит от системы вместе с дислоцированным в нем очагом возмущения. За счет захваченной в потенциальной форме энергии тело совершает следующие циклы разгона и выходит на расчетную скорость свободного движения, пропорциональную скорости ударника. Локализованные в пространстве тел «немерные» остатки волн возмущения в послеударный период вызывают пространственные и внутренние колебания ударника и ударяемого тела.

4.3Модель реактивного движения

Принципиально схема организации реактивного движения подобна рассмотренной схеме динамически функционирующего составного тела при соударении стержней. Отличие состоит лишь в том, что возмущение промежуточного упругого элемента происходит не за счет внешних сил со стороны движущихся тел, а, напротив, за счет внутренней энергии расширения самого элемента.

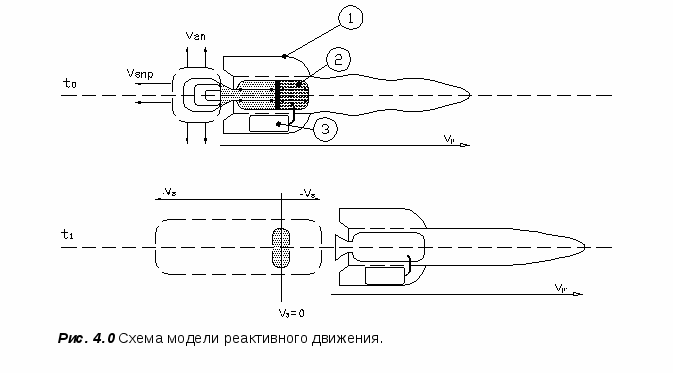
Процессы, сопровождающие реактивное движение, отражены на рисунке 4.4. Реактивный снаряд 1 получает импульс движения во время сгорания порции топливной смеси в камере сгорания 2, соединенной с емкостью топлива 3. В результате химической реакции окисления топлива резко возрастает объём продуктов горения,что, в свою очередь, вызывает интенсивный рост кинетической энергии частиц, заключенных в этом объёме. Двигаясь прочь от очага горения, эти частицы отдают свою энергию движения с одной стороны через стенки камеры горения всей массе снаряда и с другой стороны газовому объёму, имеющему возможность свободного выхода в пространство через открытые сопла. По тому, как это было показано для соударяющихся стержней, к данному моменту времени можно приурочить существование динамически функционирующей единой системы: продукты горения очаг горения торец камеры горения. Если очаг горения представить себе в виде предельно сжатой пружины, то весь процесс передачи механической энергии посредством волны деформации и последующего разгона взаимодействующих тел будет в точности повторять картину, рассмотренную применительно к соударяющимся стержням.

Интересно отметить, что выброшенный в пределы камеры горения объём топлива практически лишается механической связи с системой несущего его снаряда и до момента зажигания короткое время движется с унаследованной скоростью движения системы. C точки зрения возможного взаимодействия этого ставшего самодостаточным материального субъекта с соседними и их деформации, торцевая поверхность последних всегда будет характеризоваться нулевой скоростью.

В соответствии с этим события, отраженные на схеме рис.4.4, можно прокомментировать следующим образом.

К моменту t₁ сработало зажигание; волна расширения распространилась на весь объём продуктов горения; в центральном сечении этого объёма сформировалась зона максимального (для данного процесса) сжатия со скоростью перемещения в пространстве, равной нулю. Распространяясь влево от нулевого сечения и не встречая препятствий, волна сжатия трансформируется в волну растяжения и инициирует истечение с большой скоростью парогазовой смеси через сопла в свободное пространство. Двигаясь вправо и используя нулевое сечение как плоскость опоры, волна сжатия достигает границы камеры сгорания и, свободно её преодолевая, распространяется на тело снаряда. Вышедшая за пределы камеры часть объёма газов, получает возможность расширения в поперечном направлении и теряет скорость в продольном, как это показано на рисунке.

К моменту t₂ в результате отражения волны сжатия от свободных поверхностей снаряда и трансформации её в волну сплошного растяжения, снаряд получает приращение скорости и перемещается вправо с новой скоростью V_р1. Оказавшись в свободном пространстве, движущийся влево объём газа расширяется и теряет скорость продольного движения. В свою очередь оказавшись за пределами камеры, предельно сжатый ранее объём зависает в пространстве, парогазовая смесь конденсируется и, взаимодействуя с атмосферой медленно рассеивается. Это явление мы имеем возможность наблюдать ежедневно, провожая взглядом пролетающий на большой высоте рейсовый реактивный самолет. За пролетевшим самолетом тянется белоснежный шлейф, который в течение длительного времени не меняет своего положения в пространстве. И лишь по истечению этого времени смещается и рассеивается в пространстве сообразно движениям атмосферы.

4.4Баланс энергии при соударении

В соответствии с фазовым анализом состояний тел при соударении можно представить баланс распределения механической энергии с привязкой ко времени и пространству каждой фазы.

В исходном положении в избранных системах координат, как ударник, так и ударяемое тело характеризуется количеством движения p = mv и, соответственно, кинетической энергией T = mv²2 и сбалансированной внутренней энергией.

При сближении и динамическом контакте тел возникает площадка взаимодействия, и организуется канал для перетока и трансформации энергии движения. Как отмечалось в описании динамических моделей соударения, при сближении плоскостей стержней возникает взаимодействие односторонне свободных молекулярных поверхностей. В соответствии с фундаментальным законом притяжения – отторжения (отталкивания) между молекулами граничного слоя возникают электрические (полевые) силы отталкивания, препятствующие безграничному сближению. Граничный слой смещается внутрь тела, деформирует пространственную (кристаллическую) решетку всесторонне связанных молекул и тем самым инициирует упругость и порождает силы реакции. Отступая назад, граничные сечения укорачивают стержни и тем самым дают им возможность свободно перемещаться в пространство друг друга.

Сжатые торцы аккумулируют внутреннюю потенциальную энергию местной деформации, пока никак не изменяя внешнюю кинетическую энергию продолжающих двигаться всей массой тел.

Механическая энергия местной деформации каждого из тел измеряется линейной скоростью противной стороны и величиной собственной деформации L. На данном этапе функционирует пара: движение одного деформация другого. Эту фазу можно охарактеризовать как отражение границ.

В

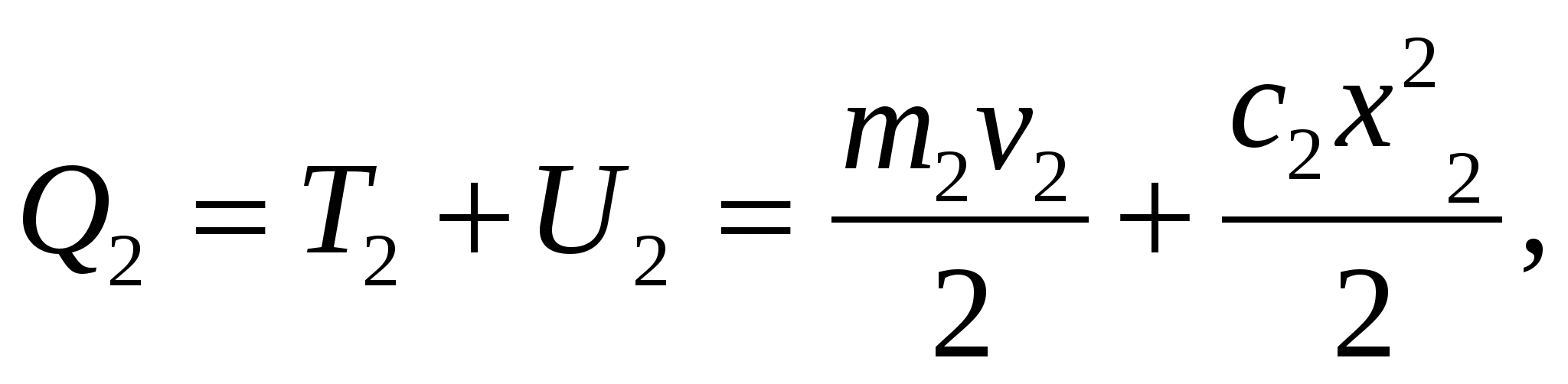
результате суммарная механическая энергия взаимодействующих тел возрастает на величину деформации

где c – жесткость тел, x – координата деформации.

Эта депонированная внутренняя энергия сыграет свою роль в процессе передачи энергии движения от тела к телу и возвратится в место своего происхождения после восстановления размеров тела и его внутреннего равновесия.

При возникновении поперечной объёмной деформации и последующей разгрузке сечений неизбежны потери на тепло и пластические сдвиги – А₁.

В результате развития волны сплошного сжатия и укорочения стержня происходит трансформация кинетической энергии в потенциальную энергию сжатия и через механизм сплошного растяжения – обратно в кинетическую

T₁ C₂x₂²2 T₂, при этом T₂ < T₁.

Так как этот процесс сопровождался распространением поверхностных массовых возмущений, то неизбежны дальнейшие потери энергии на тепло и гистерезис – А₂.

После исполнения циклов разгона в теле локализуется «немерная» часть волны возмущения и волна сплошного растяжения тела. Суммируясь, они вызовут сначала чередующиеся растяжения торцовых объёмов, а затем симметричные колебания массы тела относительно своего центрального сечения с частотой собственных колебаний. Это вызовет дополнительные потери на тепло и вибрацию – А₃ и А₄.

Схематически весь энергетический процесс соударения выглядит так:

T₁ T₂ + A₁ + A₂ + A₃ + A₄, при этом Т₂ < T₁.

Из всего изложенного ясно, что о полном обмене энергией и скоростями при соударении не может быть речи при любых обстоятельствах.

Как наглядно демонстрируют схемы динамических моделей соударений, благодаря волновому характеру распространения возмущений и соответствующим ответным реакциям среды, поле скоростей точек тела становится неоднородным. В областях, уже охваченных деформацией, возникают новые скорости, в остальной же части (где может оказаться и центр тяжести) сохраняется прежняя скорость. В связи с этим выражение закона количества движения тела, принятое в классической механике, представляется неприменимым к телу, претерпевающему изменение своего механического состояния, или, другими словами, к анализу механических переходных процессов. Формула количества движения в классической механике:

J = mv_G,

где v_G – мгновенная скорость центра тяжести тела, m – масса всего тела.

С точки зрения динамики процесса (соотношения массы и скорости) движение с момента наступления контакта можно представить, как движение тела, масса которого стремится к нулю, а скорость – к бесконечности. С момента отражения волны сжатия и в процессе развития сплошного растяжения масса вещества, вовлеченная в движение, непрерывно растет от нуля до номинального значения, а скорость, соответственно, уменьшается от максимума до номинального своего значения.

В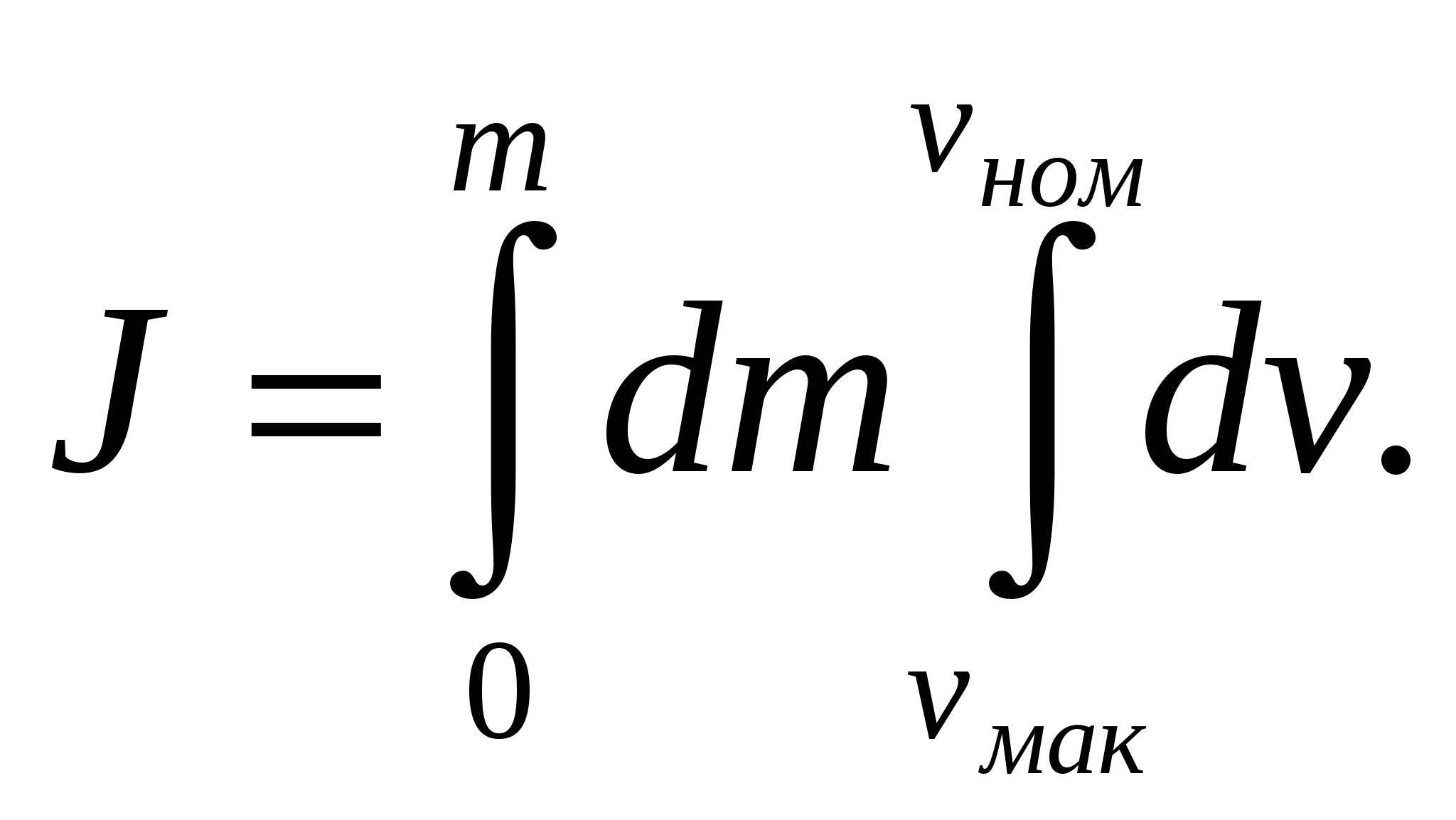
этом плане количество движения в общей форме должно выражаться как

С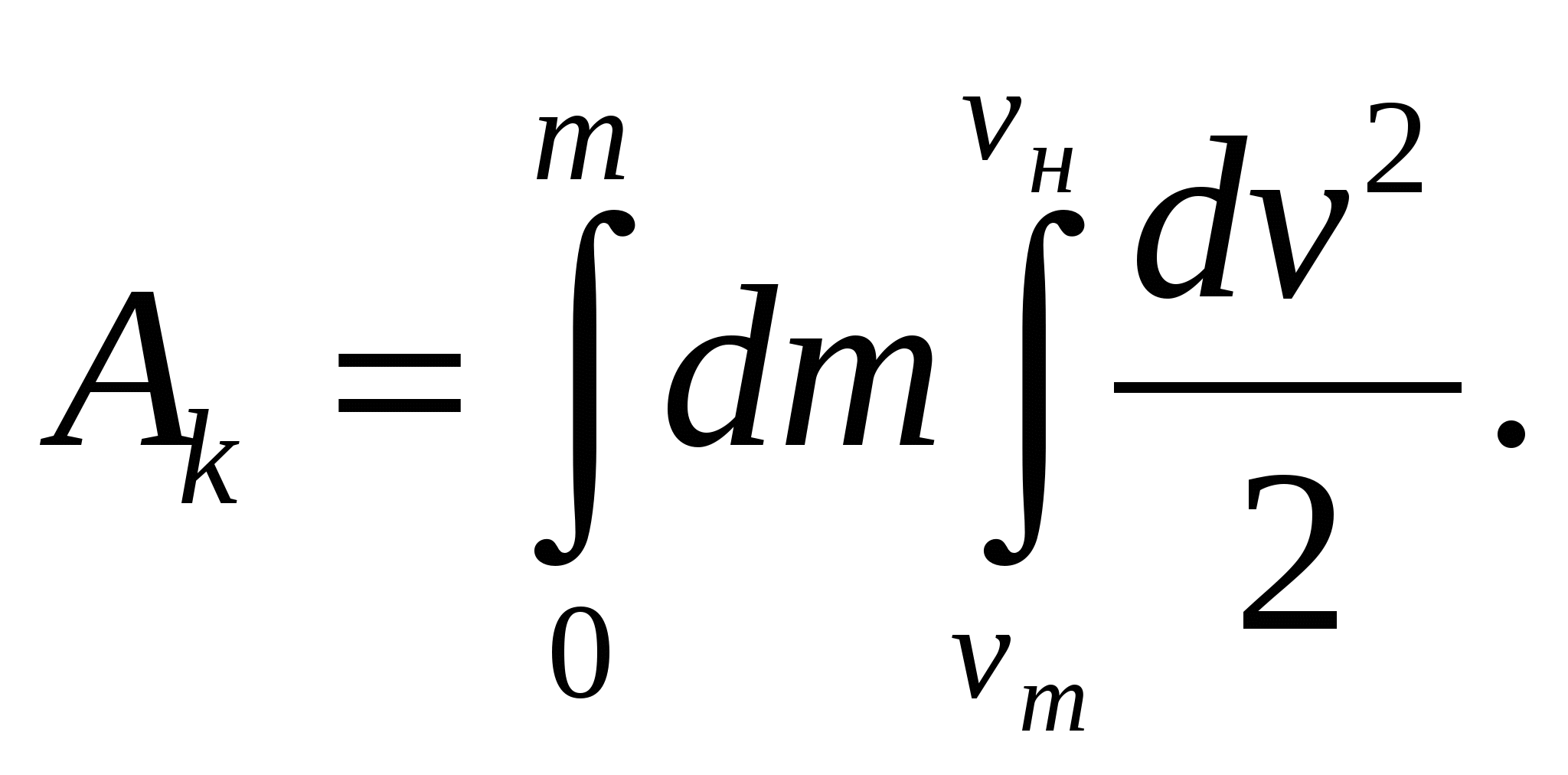
оответственно, кинетическая энергия как переменная величина в процессе развития соударения

Но при этом опять нужно иметь в виду, что приведенные соотношения относятся к переходному режиму той части тела, которая подвергается изменениям, и не имеют никакого отношения к той части, в пространстве которой в данное время ничего не происходит. В принципе суммирование энергии, локализованной в разных координатах тела и разной по времени, не выдерживает критики. То, что пришли в движение локомотив и два ближайших к нему вагона, еще ни в коей мере не означает, что поезд тронулся.

Суммирование энергии имеет смысл лишь в том плане, что энергия сохраняется в целом, хотя и пребывает в разных ипостасях.

4.5Передача энергии движения группой тел

Физике давно известен феномен передачи кинетической энергии ударяющего тела ударяемому через группу промежуточных тел, которе при этом не изменяют своего положения.

Гюйгенс сформулировал по этому поводу один из своих принципов:

«Покоящееся тело получает от движущегося неравного ему тела тем больше движения, чем больше промежуточных тел включено между двумя данными телами…»

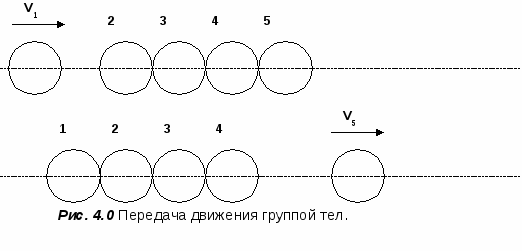
Е.В.Александров и В.Б.Соколинский (9) уточнили, что эффективность передачи энергии группой тел зависит от соотношения масс промежуточных элементов и их конфигурации. Наилучший результат при введении промежуточного элемента получается тогда, когда массы в ударной системе изменяются монотонно, то есть, убывают или возрастают.

Для системы из трех тел это условие записывается так: коэффициент передачи энергии от массы m₁ к массе m₃ через промежуточный элемент m₂ будет максимальным при

m₁ > m₂ > m₃

m₁ < m₂ < m₃.

Кроме того, передача энергии удара в системе оказывается наилучшей, если масса промежуточного элемента составляет среднее геометрическое от масс крайних элементов, или, если массы элементов системы составляют геометрическую прогрессию, члены которой m₂ = m_iq и m₃ = m₁q²,

о
ткуда показатель прогрессии

Из этого выражения следует, что показатель прогрессии q может быть больше единицы, если массы элементов системы возрастают, и меньше единицы, если массы убывают.

Е
сли заданы массы начального и конечного i-того тел, а также общее количество тел системы i, то показатель прогрессии

К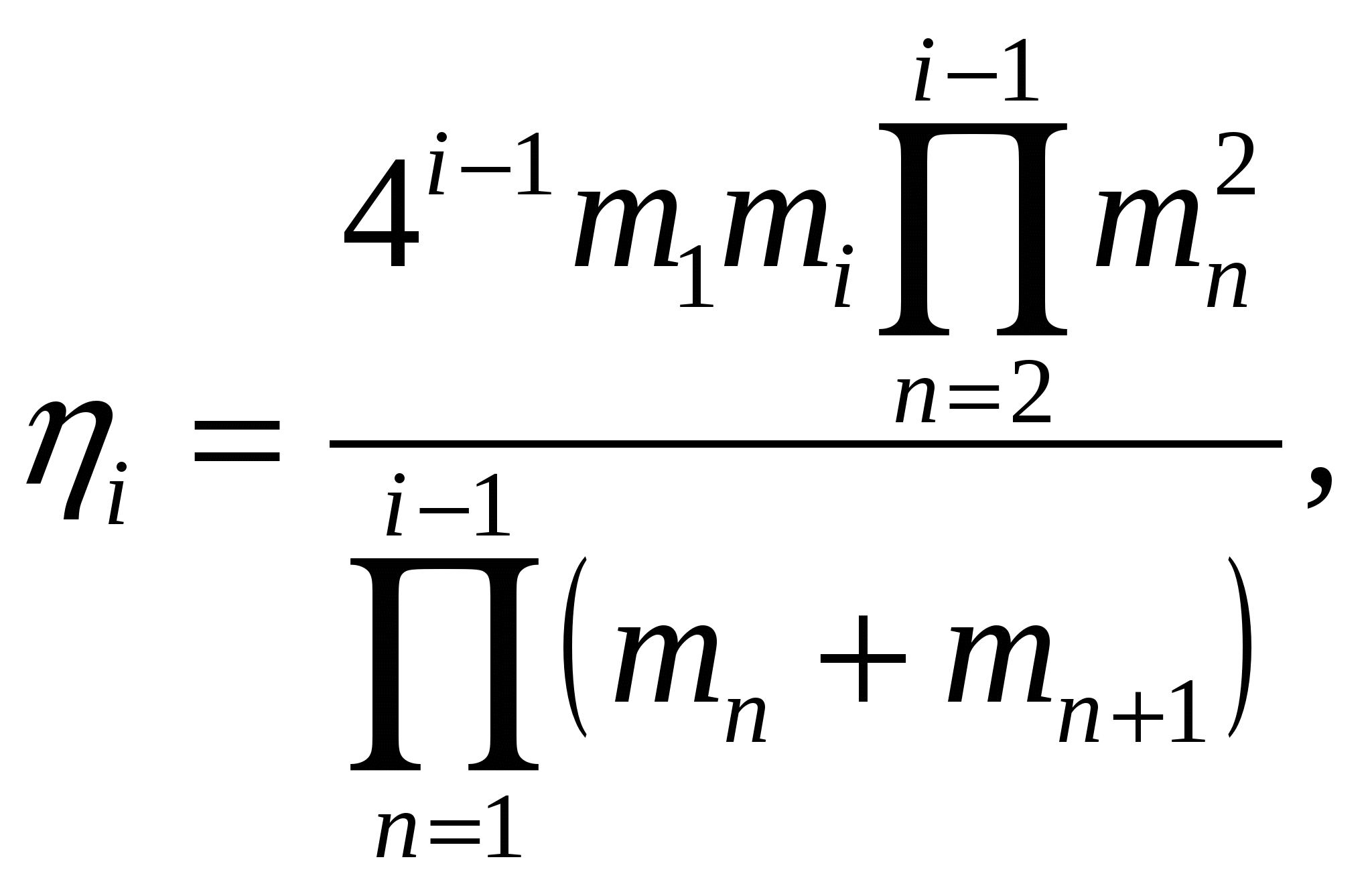
оэффициент передачи энергии удара системы из i-тел

где


- знак произведения.

Полученные решения относятся к системам, в которых реализуется последовательное соударение тел (пар тел). Расчет такой системы сводится к последовательному расчету серии элементарных двухмассовых систем. Если же происходит одновременное соударение нескольких элементов, то анализ такой системы возможен только с привлечением теории упругости.

Для уяснения физической картины происходящих процессов в ходе канализации энергии движения через промежуточные элементы рассмотрим динамическую модель шарового волновода, приведенную на рисунке 4.6. На основе уже сформулированных положений в отношении соударяющихся стержней отметим характерные моменты, присущие упругому волноводу, составленному из прижатых и пребывающих в акустическом контакте стальных гладких шаров. Выделим в цепи совершающихся событий узловые специфичные для данного момента и данного места условия и эффекты и определим причинно-следственную связь их с предыдущими и последующими событиями. В последующем привяжем соответствующие эксперименты к месту и содержанию полученных данных. Надежный контакт шаров в течение времени реализации удара можно обеспечить известными способами: магнитным полем, подвесом на тонких нитях и т.п.

Итак, сформулируем состояния, применительно к каждой из выделенных временных точек и каждой соответствующей им координате.

Время t₁. Шар1 со скоростью V₁ вошел в динамический контакт с системой. В результате его внедрения в пространство шара 2 в теле последнего сформировалась площадка динамического контакта, диаметр которой определяется глубиной предельного сжатия. В обе стороны от зоны предельного сжатия начала движение волна деформации. В отличие от стержней она носит характер объёмной волны расширения, то есть одновременно с продольным движением деформации развивается деформация в поперечном направлении. Так как поперечная волна организуется через механизм сдвига сечений, то она оказывается сдвинутой по фазе и по времени относительно продольной волны и отстает по скорости распространения в теле шара. В связи с этим следует ожидать, что продольная волна, параметры которой определяются диаметром площадки динамического контакта, прибудет к свободной поверхности шара раньше.

Время t₂. Волна сплошного объёмного сжатия распространилась до поперечного диаметрального сечения шара и, отражаясь от свободной поверхности в верхней и нижней частях полушария, трансформируется в волну сплошного продольного растяжения вправо. Шар-ударник 1 деформируется, испытывая сжатие справа со стороны шара 2 и слева за счет движения левой еще не деформированной части.

Время t₃. Оба контактирующие шара достигли максимальной для данных условий статической деформации объёмного сжатия. В их телах возникли встречные силы реакции, стремящиеся восстановить первоначальную форму. Всей своей массой шар1 приобрел нулевую скорость. Влево организуется волна сплошного растяжения. Между шарами начинает формироваться площадка динамического контакта. Правое полушарие шара 2 испытывает сжатие от восстановления формы и одновременно массовую волну растяжения за счет отражения волны сжатия от свободной поверхности выше и ниже площадки динамического контакта. Через сжатый приконтактный объём с опережением в тело шара 3 проследовал импульс сжатия, возникший в момент касания ударником поверхности левого полушария шара2.

Следом идет более мощный растянутый во времени импульс сжатия, обусловленный суммарным действием реактивных сил восстановления формы и массового движения части шара-предшественника. Шар3 как бы получает удар от шара 2, но механика этого удара отличается от первоначального тем, что здесь отсутствует пространственный разрыв между телами, и волна возмущения проходит через предварительно сформировавшийся переходный контакт без искажения, как по сплошному телу.

Время t₄. В результате восстановления формы шаров 1-2 возникли реактивные силы, как показано на схеме модели. Это, в свою очередь, вызвало растяжение поверхности шара 1 и дальнейшую трансформацию энергии сжатия шару 3. Шар 2, разгружаясь, также стремится вернуться в первоначальное состояние. Голова продольного импульса сжатия переместилась в пространство шара 4.

Время t₅. Отраженные от поверхности шаров волны растяжения возвращаются в форме возмущения сжатия, в результате чего возникают продольно-поперечные массовые волны вещества, которые движутся от места своего возникновения к точке диаметра и, в силу своей природы быстро затухают. Они поочередно возникнут по мере развития эволюций на всех участвующих в передаче движения телах. Деформация объёмного сжатия охватывает шары 3 и 4, и они повторяют движения предыдущей пары.

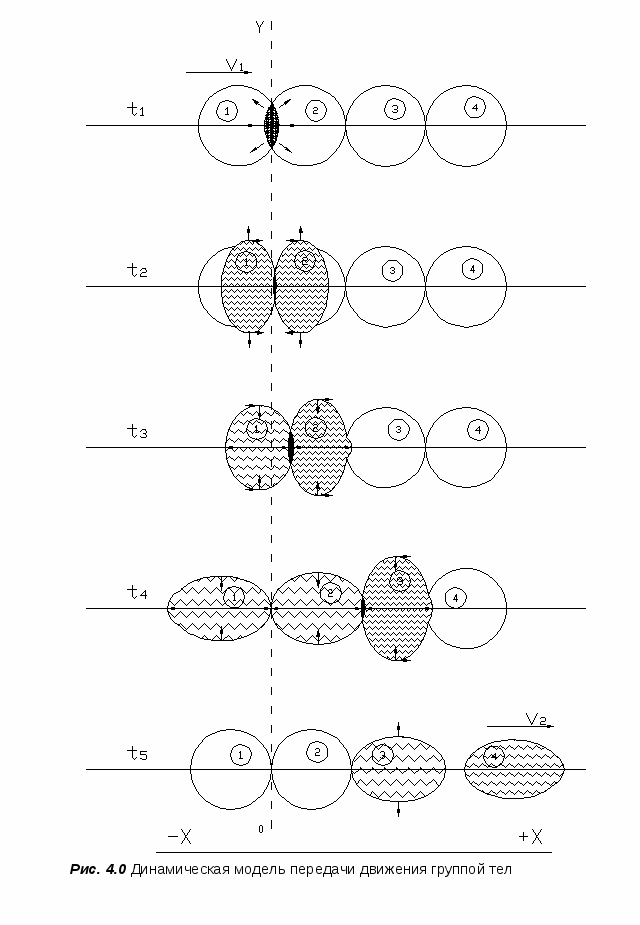
Время t₆. Деформация объёмного сжатия, наконец, достигает тела последнего шара в системе, отражается от его поверхности и трансформируется в деформацию сплошного растяжения. Как только скорости всех точек тела примут одно значение, шар отходит от системы, совершает скачки ускорения в соответствии с параметрами удара и выходит на свою расчетную скорость V₂ < V₁. Продолжая движение, он восстанавливает первоначальную форму, вибрирует и несколько нагревается. Промежуточные тела, оставаясь на своих местах, также восстанавливают форму, вибрируют и нагреваются.

Приведенная схема шарового волновода наглядно демонстрирует принципиальную возможность канализации энергии движения по волноводам любой конфигурации. На рисунке 4.7 приведен пример такого волновода, выполненного в виде изогнутой трубы, заполненной плотно пригнанными упругими шарами. Схематически показано движение волны возмущений по волноводу после приложения импульса внешней нагрузки Р.

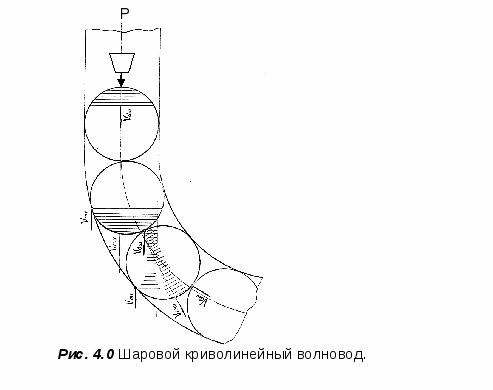
Глава 5 Экспериментальное исследование процесса динамического контактного взаимодействия

5.1Обзор распространенных схем

Несмотря на большое количество экспериментальных данных по исследованию процесса соударения тел, накопленных к настоящему времени (8, 9, 10, 12, 34, 35, 36, 39, 45), остаются спорными вопросы о величине напряжений, деформации и смещении граничных слоев в зоне контакта, продолжительности процесса соударения, характере и продолжительности вторичных явлений, вызванных ударом.

Недоступность очага деформации при ударе для инструментальных средств, быстротечность процесса, малые массы вещества и их высокая скорость на этапе формирования ударных волн не позволяют с достаточной степенью точности и повторяемости экспериментально определить основные параметры соударения.

В связи с этим Н.А.Кильчевский (23) замечает:

«Продолжительность удара является до последнего времени единственной характеристикой движения соударяющихся тел, поддающейся непосредственному измерению».

Знание продолжительности динамического контакта и создание достоверной модели процесса открывают широкие возможности для определения параметров соударения и уточнения теоретически установленных закономерностей.

Для измерения параметров соударения различными экспериментаторами создан ряд быстродействующих приборов и устройств, в которых использованы самые эффективные достижения баллистики, электроники, оптики, радиолокации, научного кино.

Кратко рассмотрим наиболее характерные примеры.

Прежде всего, следует назвать принцип и устройство, предложенные одним из первых исследователей анатомии удара Б.Гопкинсоном.. «Мерный стержень Гопкинсона» позволил приблизится к пониманию природы передачи движения твердым телом и получить данные, количественно характеризующие удар. Это устройство было использовано для исследования распространения импульса напряжения и природы зависимости давления от времени при взрыве или встрече снаряда с жесткой поверхностью. На рисунке 5.1 приведена схема прибора Гопкинсона.

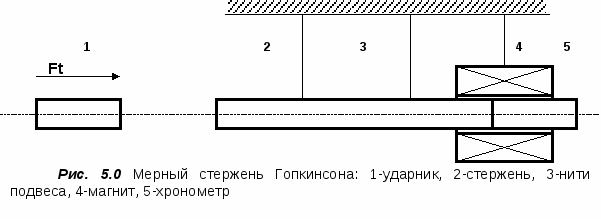
Стальной цилиндрический стержень длиной около метра или более и около 2,5 см в диаметре подвешен горизонтально с помощью нитей так, что он может совершать колебания в вертикальной плоскости. К одному концу стержня прижат с помощью магнита притертый стержень, названный «хронометром»; к другому концу прилагается переменное давление от взрыва заряда или от летящего ударника.

В изложении Г.Кольского, в представленной схеме протекают следующие процессы. При нанесении возмущения на ударяемый конец вдоль стержня начинает распространяться импульс сжатия, который будет распространяться без искажения, если диаметр стержня мал, а материал стержня не напряжен выше предела пропорциональности. Импульс сжатия проходит без изменения формы через место стыка стержня и «хронометра», а затем отражается от свободного конца «хронометра» в виде импульса растяжения. Отраженный импульс растяжения распространяется через хвост падающего импульса сжатия, и как только на стыке стержня и «хронометра» возникает растягивающее напряжение, этот последний отлетает с моментом количества движения, захваченного им.

В опытах Гопкинсона количество движения измерялось путем захвата «хронометра» в баллистический маятник, а количество движения, сохранившееся в стержне, определялось по амплитуде его колебаний.

Дальнейшее развитие эта идея получила в устройстве, предложенном Р.Девисом (рис.5.2). С усовершенствованной электрической схемой его применил Г.Кольский для определения зависимости напряжение – деформация в образцах, имеющих форму диска (8).

М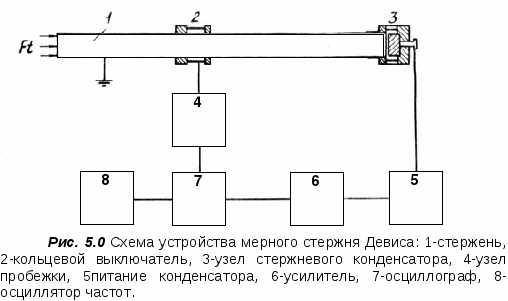
ерный стержень Р.Девиса обеспечивает непрерывную запись предельного перемещения, производимого импульсом давления на свободном конце стержня. Для этого на стержне 1 установлен кольцевой выключатель 2 и на торце, противоположном прилагаемой нагрузке Ft, узел стержневого конденсатора 3. Продольное перемещение концевого сечения стержня измеряется путем использования стержня в качестве заземленной обкладки в плоском конденсаторе. Изолированная обкладка состоит из металлической пластинки вмонтированной в узел стержневого конденсатора. Этот узел свободно скользит по концу стержня и содержит изолированную пластинку, параллельную концевому сечению стержня. При медленном движении стержня обе обкладки движутся вместе, при приходе же импульса конец стержня перемещается свободно, тогда как изолированная пластинка вследствие ее инерции в течение короткого промежутка времени остается в покое. Изолированная пластинка заряжается до высокого напряжения с помощью узла питания конденсатора 5. Он содержит контур сопротивление – емкость с большой постоянной времени, так что заряд изолированной пластинки может изменяться только очень медленно, и поэтому быстрое изменение емкости плоско – параллельного конденсатора приводит к соответствующим изменениям разности потенциалов между его обкладками. Если относительное изменение емкости мало, эта разность потенциалов прямо пропорциональна перемещению концевого сечения стержня. Эти изменения разности потенциалов усиливаются и регистрируются на катодно-лучевом осциллографе.

Горизонтальным перемещением луча осциллографа управляет узел пробежки 4, который включается инерционным выключателем на стержне. Выключатель состоит из изолированного металлического кольца, которое свободно скользит по стержню и находится в контакте с металлическими штифтами, ввинченными в стержень. При взрыве заряда на торце стержня набегающий импульс давления отделяет кольцо от штифтов, что приводит к запуску узла пробежки.

С помощью описанного мерного стержня Девис установил продолжительность ударных импульсов при зарядах различной интенсивности, а также наличие высокочастотных колебаний в импульсе.

Г.Кольский (8) дает следующую обобщенную классификацию методов, используемых для экспериментального исследования динамического поведения твердых упругих тел:

• метод свободных колебаний,

• резонансный метод,

• метод распространения волн,

• прямое определение кривых напряжения – деформация.

Особое внимание при экспериментальном исследовании параметров удара уделяют измерению продолжительности удара, так как знание этой величины и скорости распространения волн для данной среды открывает возможности вычисления ряда прочностных характеристик, а также характера динамического поведения взаимодействующих тел.

Из старых методов, которыми пользовались Сирс и А.Н.Динник, Кильчевский (25) отмечает метод баллистического гальванометра предложенный Пуйлье. При соударении твердых тел цепь гальванометра замыкается и начинается измерение количества протекающего за время существования контакта электричества (при стабилизированных параметрах цепи и стабильном напряжении питания). Отмечается, что этот метод является грубым, так как фиксирует геометрический, а не динамический контакт. Кроме того, возможен пробой промежутка между контактами до наступления геометрического контакта, на точность измерений влияет инерционность гальванометра и т.д.

В опытах Н.Н.Давыденкова (9) использован акустический метод. Акустические колебания, возникающие в результате возмущения поперечных колебаний исследуемого стержня, измерялись с помощью настраиваемой в унисон стальной струны реохорда. Зная высоту тона стержня, по известной формуле, определяли модуль упругости. Эти опыты Давыденкова подтвердили практическое совпадение значений статических и динамических модулей упругости.

Для исследования поперечного удара падающего груза о балку Туци и Низида (9) применили киносъёмочную аппаратуру, в которой пленка перемещалась со скоростью 24мсек, а время экспозиции составляло 180000 секунды. С помощью этой аппаратуры зафиксированы повторные удары при взаимодействии падающего шара и балки, теоретическое объяснение которых остается предметом обсуждения.

Б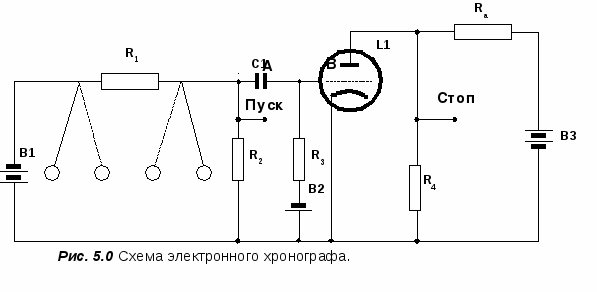
ольшой интерес для уяснения динамики упругих тел при соударении представляют результаты опытов, проведенных Б.М.Малышевым (34) с помощью электронного хронометра, пусковая схема которого приведена на рис. 5.3. К концам сопротивления R₁ подсоединены соударяющиеся тела. В момент начала соударения сопротивление R₁ закорачивается, ток в пусковой цепи скачком возрастает, и с сопротивления R₂ снимается импульс для запуска хронографа. В момент размыкания напряжение на R₂ скачком принимает прежнее значение. Малые сопротивление R₃ и емкость C служат для дифференцирования входного напряжения. При закорачивании R₁ на сетку лампы подается отрицательный импульс. В этот момент изменения тока в анодной цепи не происходит, так как лампа в обычном состоянии заперта. В момент размыкания на сетку лампы подается положительный импульс, лампа отпирается, и с анодной цепи снимается отрицательный импульс для остановки хронографа.

Нужно отметить, что в данной схеме, как и в описанной выше с гальванометром, факт динамического взаимодействия фиксируется с помощью электрического контакта, поэтому остаются в силе высказанные ранее замечания. Хотя этот метод не может дать полностью гарантированной абсолютной величины времени динамического контакта он позволяет получить чрезвычайно важные относительные показатели удара при различных значениях длины и скорости ударника.

При испытаниях стержни подключали к хронографу и располагали соосно на плоскости. Удар производили, перемещая рукой один из стержней. Стальные шары подвешивали при помощи длинных V-образных подвесов из тонкой стальной проволоки, для удара один из шаров отводили с помощью нити, которая пережигалась.

В таблицах 5.1 и 5.2 приведены полученные с помощью хронографа результаты экспериментов.

Из данных, приведенных в таблицах, следует, что время соударения определяется длиной ударника. Получен график зависимости продолжительности удара для стержней различной длины, из которого следует, что для длин L>100 см существует строго прямолинейная характеристика.

Таблица 5.1

Номер стержня	Длина стержня, см	Показатели хронографа 10-5 сек
1 – 4	202,4 – 156,8	77 77 77 76 76 77 76 77 77
2 – 4	187,5 – 156,8	71 72 72 72 72 73 73 72 73
3 – 4	172,5 – 156,8	68 66 66 68 67 67 67 66 66
1 – 5	202,4 – 125	77 76 76 77 77 76 76 77 77
2 – 5	187,5 – 125	73 72 72 71 72 72 72 72 71
3 – 5	172,5 – 125	65 66 66 65 65 65 65 65 66
4 – 5	156,8 – 125	61 60 60 61 61 60 60 60 61

Таблица 5.2

Номер стержня	Продолжительность соударения, 10-5 сек	Скорость упругих волн
1	76,7	5270
2	72	5215
3	66,1	5200
4	60,4	5190

При сбрасывании латунного стержня диаметром 6мм и длиной 1425мм на цилиндр диаметром 76мм и длиной 104мм с высоты 5 – 2000мм (высота менялась с интервалом в 100мм) для продолжительности удара по хронографу получался один и тот же отсчет – 84 1. На основе этого сделан вывод о том, что при упругих деформациях время удара не зависит от скорости соударения. Однако в упомянутом эксперименте с шарами в случае сравнительно малых скоростей отчетливо просматривалась зависимость времени соударения от скорости.

Е.В.Александров и В.Б.Соколинский (11, 9) исследовали процесс соударения различной длины цилиндрических стержней с помощью тензодатчиков, наклеиваемых на ударяемое тело.

На рис5.4 приведена схема и таблица результатов одного из таких экспериментов. Из рассмотрения соответствующих каждой точке осциллограмм и средних величин напряжений, приведенных в таблице, видно, что напряжения в точках (исключая приконтактную зону) за все время прохождения ударного импульса сохраняют практически постоянное значение и мало отличаются друг от друга по величине. Отсюда авторы делают вывод о плоском характере фронта ударной волны.

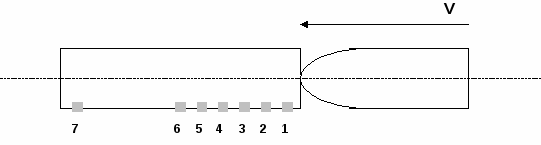
Таблица 5.3

Номер датчика	Расстояние от торца абс. H	Расстояние от торца отн. Hr	Амплитуда напряжений кгсм2
1	10	0,6	-38
2	20	1,2	155
3	30	1,8	225
4	40	2,4	238
5	50	3,0	242
6	60	3,6	246
7	120	7,2	248

Рис. 5.1 Cхема эксперимента и таблица результатов измерений

Отметим ряд принципиальных выводов, к которым пришли авторы на основе проведенных экспериментов:

Действие ударной нагрузки не передается мгновенно всем частям тела.

Скорость перемещения частиц тела (массовая скорость) пропорциональна напряжению, тогда как скорость распространения самой волны не зависит от напряжения, а зависит только от модуля упругости и плотности материала.

Качественная сторона ударного процесса и его математическое описание позволяют интерпретировать систему соударяющихся стержней как систему колебательную, в которой стержневые части представляют собой линейные колебательные элементы, присоединенные к торцовому контуру, который не всегда является линейным.

Осциллограммы, полученные с помощью тензодатчиков, контролирующих напряжения между смежными сечениями ударяемого стержня, показывают, что величина этих напряжений зависит от скорости, а продолжительность ударного импульса – от длины ударника.

Подводя итоги проведенных различными экспериментаторами расчетов и измерений, мы можем утверждать, что они не закрыли вопросы о характере и параметрах изменений в контактной зоне, об истинной форме механического возмущения и господствующих видах деформации на различных этапах ударного процесса, о динамике разгона ударяемого тела в послеударный период.

С целью получения ответов на отмеченные вопросы автором настоящей книги были предложены некоторые новые средства измерения и разработаны методики проведения экспериментов. Их описанию посвящены последующие главы.

5.2Разработка новых технических средств и методики эксперимента

Анализ предложенной динамической модели твердого упругого тела и схемы механических эволюций тел при их соударении показал, что следует ожидать новых нетрадиционных трактовок физики процесса, поэтому возникает настоятельная необходимость их экспериментального подтверждения. Представляется целесообразным проанализировать динамику ударника, волновода и отлетающего тела в их свободном механически не связанном состоянии при отсутствии повторных воздействий, отражений волн в соединительных звеньях, колебаний этих звеньев с собственной частотой.

Чрезвычайно интересной предстала возможность анализа разгона свободного тела после усвоения силового воздействия на фоне распространяющихся волн деформации. Чистота ожидаемой картины преобразования энергии воздействия в энергию свободного движения предполагает, что встраиваемые измерительные средства органически слиты с исследуемыми телами и не влияют на развитие событий в пространстве этих тел, как в стационарных, так и в переходных режимах.

Изложенным требованиям подчинены разработанные технические средства и схемы их использования.

5.2.1 Устройство для измерения механических силовых импульсов

Устройство (61) предназначено для изучения механических возмущений, возникающих при однократном ударе по мерному стержню, а также эволюций движения, которое испытывает отлетающее тело в послеударный период. На рис.5.5 приведена схема устройства и его составные части.

Как это видно на рис5.5, предложенная автором схема является развитием рассмотренной ранее идеи Гопкинсона. Главной отличительной особенностью предложенной схемы является то, что отлетающее тело (хронометр) выполнено электрически чувствительным за счет встройки в разрезы хронометра на выбранных расстояниях пьезоэлектрических дисков из титаната бария или цирконата-титаната свинца. Подробнее конструкция хронометра будет рассмотрена дальше.

Ударник 2 на подвесе 1 отклоняют на некоторый угол, например, с помощью нити, которая затем пережигается. Получивший свободу шар разгоняется и наносит однократный удар по системе. Сформировавшаяся на ударяемом конце волновода 3 волна сжатия распространяется вдоль его тела, преодолевает границу стыка волновода и хронометра, проходит по телу упругих цилиндров и пьезометрического диска, составляющих хронометр, а затем отражается от свободной поверхности хронометра и трансформируется в волну растяжения.

Чтобы избежать искажений при прохождении механического возмущения через стыки, поверхности контакта притирают и смазывают машинным маслом. В случае использования магнита для удержания хронометра его торцовые поверхности также обрабатывают и смазывают. Это обеспечивает надежный акустический контакт в цепи распространения ударной волны.

В процессе прохождения однократного ударного импульса пьезометрический диск претерпевает следующие фазы своего механического состояния: сжатие – разгрузка – растяжение. Электрический сигнал (величина э.д.с.), соответствующий этим фазам, подается на регистрирующий прибор 7. В случае использования магнитной шайбы в зависимости от ее силы притяжения и интенсивности удара возможны два режима для хронометра: отрывный и безотрывный. При отрыве хронометр «захватывает» часть движения импульса, отрывается от волновода и продолжает свободный полет, совершая определенные эволюции своего движения и посылая соответствующий сигнал в электрическую схему измерения. Оставшиеся ударник 2 и волновод 3, взаимодействуя, совершают определенные движения и инициируют соответствующие им волны деформации, однако они уже не фиксируются и не влияют на показания регистрирующего прибора. В безотрывном варианте вызванная ударом волна деформации многократно отражается в системе и регистрируется измерительным прибором.

Т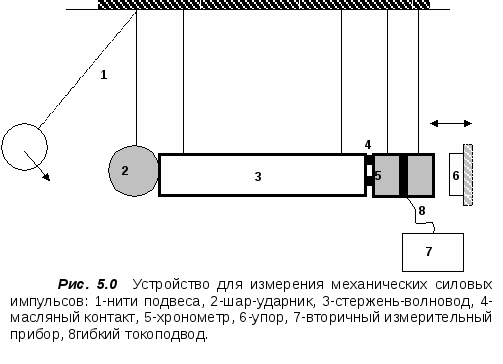
аким образом, предложенная конструкция устройства выгодно отличается от известных тем, что она позволяет провести импульс механического возмущения непосредственно через измерительный датчик при одинаковых условиях с присоединенным телом и получить прямой электрический сигнал об импульсе, избежав накладки поверхностных явлений и других вторичных наложений. Существенно также то, что в устройстве отсутствуют механические крепежные детали, которые бы вызывали дисперсию и разветвление возбужденной ударом волны.

5.2.2 Пьезоэлектрический хронометр

Пьезоэлектрический хронометр представляет собой составное сплошное цилиндрической формы тело, главным чувствительным элементом которого является пьезокерамический диск. Соединение всех составляющих его элементов в монолит осуществляется с помощью упругой связки типа эпоксидной смолы.

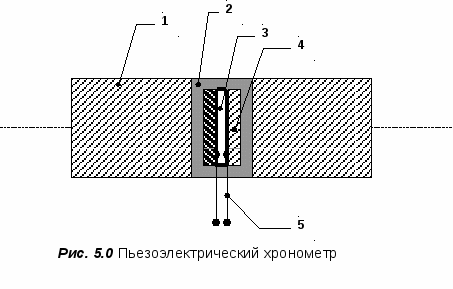
На рис.5.6 показана конструкция устройства, где 1-цилиндры стальные, 2-заливка эпоксидная, 3-пьезокерамический диск, 4-стеклотекстолит, 5-токосъёмники. В качестве токосъёмников использовали луженый провод или фольгу, которые предварительно припаивались к посеребренной поверхности диска. Стеклотекстолитовые диски 4 служат для изоляции датчика 3 от корпуса измерительного устройства. После заливки связки конструкция выдерживается под прессом до полного затвердевания связки и ее стабилизации. Торцы цилиндров шлифуют, соблюдая повышенные требования к плоскостности и минимуму шероховатости.

Представленную конструкцию хронометра можно рассматривать, как самостоятельный модуль, который может использоваться в различных по назначению и конструктивному исполнению измерительных устройствах. Пример такого использования применительно к анализу работы вибротехники приводится ниже.

5.2.3 Пьезоэлектрический датчик колебаний

При испытании вибрационных и пневмоударных систем возникает необходимость фиксировать массовые перемещения рабочих органов с одновременной регистрацией механических возмущений, вызванных ударом со стороны, например, транспортируемого сыпучего материала. Серийные измерители вибрации, как пьезоэлектрические, так и других типов, такой возможности не обеспечивают. Чтобы решить упомянутую задачу, был разработан датчик, конструкция которого показана на рис.5.7.

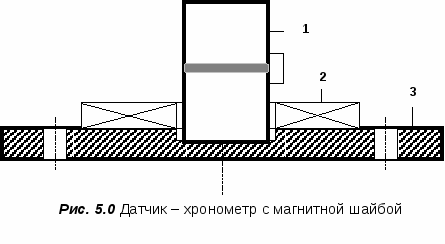
Основные элементы датчика: 1-хронометр с клеммником, 2-постоянный магнит – шайба, 3-фланец. Хронометр устанавливается в выточку на фланце. Для надежного акустического контакта поверхности торца хронометра и плоскость выточки притирается и смазывается машинным маслом. Фланец датчика жестко крепится к испытуемым движущимся или неподвижным элементам (вибропитателю, бункеру и т.п.) с помощью болтов или сварки. Перед установкой датчика поверхности сопряжения зачищаются и притираются.

Датчик может работать в случае измерения колебаний без отрыва хронометра в режиме акселерометра. В случае приложения ударной нагрузки подбором усилия магнитного прижима можно устанавливать предельные нагрузки, после которых хронометр отлетает, захватывая определенную часть ударного импульса и предоставляя возможность изучения физики распространения его в свободном от связей элементе механической системы.

5.2.4 Пьезоэлектрический измеритель поверхностных возмущений

Для измерения микроперемещений на поверхности тел, испытывающих механические возмущения, разработана конструкция измерительного устройства, чувствительным элементом которого служит звукосниматель на пьезокристалле чувствительностью по частоте до 20 МГц. Звукосниматель от серийной радиоаппаратуры имеет алмазную иглу, способную копировать микроповерхность за счет смещения гибкого крепежного узла. На рис.5.8 показана конструкция измерителя поверхностных возмущений и установка его на шаровой волновод.

Измеритель крепится над исследуемой поверхностью так, чтобы обеспечивалось его относительное перемещение до соприкосновения иглы с испытуемой поверхностью, после чего создается небольшое предварительное усилие. Снимаемый с пьезоэлемента сигнал подается через согласующий операционный усилитель на осциллограф или регистрирующие амперметры или вольтметры повышенной чувствительности. Операционный усилитель работает в режиме повторителя с высоким входным и низким выходным сопротивлением, что обеспечивает неискаженную передачу сигнала пьезодатчика, имеющего высокоомное выходное сопротивление, на вход выпрямителя.

5.2.5 Шаровой испытательный стенд

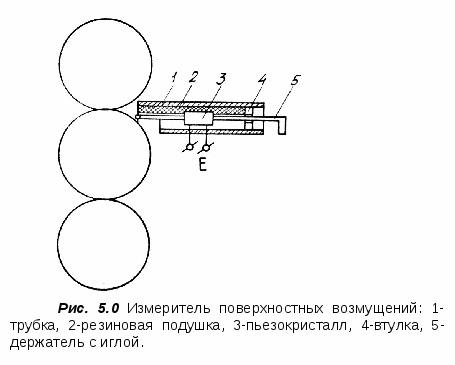
На основе представлений о закономерностях формирования и распространения ударных возмущений, выявленных с помощью динамических моделей, разработана схема испытательного стенда на основе шарового волновода.

На рис.5.9. приведена схема конструкции испытательного стенда с шаровым криволинейным волноводом. Стенд представляет собой трубчатый волновод 2, укрепленный на основании 1 и заполненный стальными полированными шарами от шарикоподшипника. Стенд имеет следующие составные элементы: индикаторы поверхностных возмущений 4, индикаторы контакта шаров 5, мерные линейки 6, ударяемое тело 7, стопорное устройство 8. Подвижное стопорное устройство выполнено в виде вилки, что обеспечивает торможение отлетающего шара и одновременно свободное движение держателя иглы пьезодатчика, сохраняющей свой контакт с поверхностью шара.

Электроконтактные датчики – индикаторы положения шаров представляют собой электроды из стальных пластин, закрепленные в изолирующих втулках, жестко установленные на трубе волновода. Пьезодатчики монтируются на жестких основаниях около измерительных отверстий в трубе волновода. При освобождении ударяемого тела (например, при пережигании нити подвеса) оно совершает свободное падение, приобретает кинетическую энергию и отдает ее при встрече с системой шаров. Возникшее механическое возмущение передается по волноводу отлетающему шару в правой части волновода и вызывает его свободный полет в канале волновода. С помощью мерных линеек фиксируют высоты падения и взлета и производят необходимые вычисления эффективности передачи механической энергии при ударе. Предварительное поджатие шаров за счет их веса обеспечивает условия для эффективного прохождения ударного импульса через граничные поверхности.

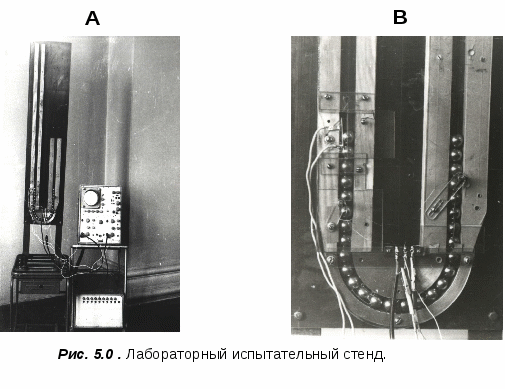
Схема стенда позволяет легко менять в процессе экспериментов длину волновода, количество промежуточных тел, включать во внутренний и оконечный контур тела других форм, измерять механические возмущения в любых выбранных точках волновода и соударяющихся тел.

На рис.5.10 приведены фотографии лабораторного испытательного стенда, изготовленного в лаборатории автоматизации металлургического комбината «Запорожсталь»: А – общий вид устройства, В – узел установки датчиков. Для удобства работы и наблюдений криволинейный канал выполнен плоским с применением деревянных реек, а нижняя часть выполнена из двух стальных точеных деталей. Лицевая сторона закрыта прозрачным оргстеклом, на котором закреплены датчики.

5.3Экспериментальное исследование волн деформации и свободного разгона тела.

Программа исследований была разработана автором и практически была реализована в 1980 – 88 году в центральной лаборатории механизации и автоматизации металлургического комбината «Запорожсталь». Автор приносит глубокую благодарность творческому коллективу работников лаборатории, занятых в подготовке и техническом обеспечении исследований, а также внедрении в производство связанных с этим новых технических решений. Считаю своим долгом также выразить особую признательность доценту Запорожской промышленной академии Борису Александровичу Воронину и Александру Кисилеву – тогда молодому инженеру – экспериментатору.

Все эксперименты проводились на базе описанных динамических моделей, средств измерений с использованием лабораторного шарового стенда и последующей проверкой полученных выводов на реально действующем оборудовании: бункерах, дозаторах сыпучих материалов, вибромашинах и т.д. Результаты исследований были положены в основу технических решений, выполненных на уровне изобретений.

5.3.1Исследования с помощью шарового волновода. Схема экспериментов Э1

К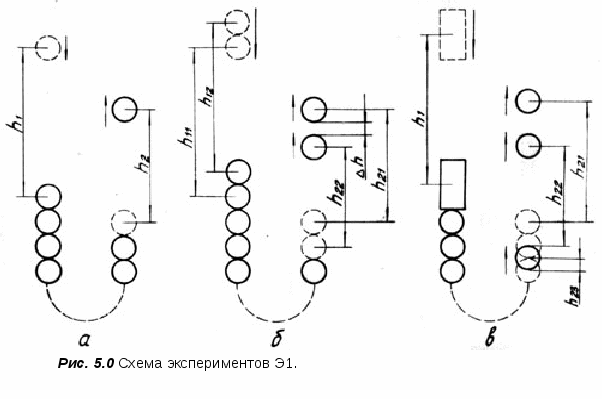
анал волновода заполнен 20-ю стальными шарами диаметром 20,5мм. Удар по системе контактирующих неподвижных шаров производится с помощью ударников различной массы и конфигурации (рис.5.11).

Э1-а. Удар шаром, d_ш = 20,5мм. Встречаясь с системой, ударник мгновенно останавливается (по визуальному наблюдению), противоположный шар взлетает вверх, система остается неподвижной.

Энергия ударника до удара определяется его начальной высотой h₁ над поверхностью ударяемого тела

A₁ = m₁gh₁

Энергия отлетающего тела в конечной точке свободного полета А₂ = m₂gh₂.

Т
ак как по условиям эксперимента m₁ = m₂, то коэффициент передачи энергии системой определяется как

Результаты измерений для различных значений h₁ и количества шаров – проводников в системе сведены в таблицы 5.4 и 5.5.

20 шаров в системе Таблица 5.4

h1	Высота отлета h2	kп
350	110	110	105	115	110	105	110	107	105	100	0,308
750	175	155	165	160	160	162	155	160	168	170	0,217
1100	240	225	220	212	210	230	190	195	210	230	0,197

Таблица 5.5

Nш	h1	Высота отлета h2	kп
20	1100	235	215	200	195	190	185	215	196	216	0,188
19	1100	182	220	205	240	215	210	201	191	180	0,187
17	1100	220	190	190	155	207	183	217	202	140	0,177

Как это видно из данных таблицы 5.4, коэффициент передачи механической энергии по волноводу существенно понижается с увеличением скорости ударника (интенсивности удара). Это можно объяснить, воспользовавшись динамической моделью данного типа соударения. Более интенсивное сжатие контактной площадки приводит к увеличению волнового сопротивления (импеданса). В результате более раннего формирования состояния предельного сжатия ударяемого тела часть энергии ударника обращается на него самого и приводит к его более интенсивной деформации, а, значит и к более интенсивному его торможению.

Уменьшение количества шаров в волноводе заметно уменьшает коэффициент передачи энергии (табл. 5.5), что полностью соответствует принципу Гюйгенса.

При сбрасывании нескольких контактирующих между собой шаров (рис. 5.11,б) справа отлетает столько же шаров и несколько сдвигается последний из оставшихся, при этом между каждым из них наблюдается промежуток Δh, свидетельствующий о сдвиге во времени начала их свободного движения. Как было показано выше, этот промежуток времени необходим для развития деформации растяжения, в результате которой появляется массовая скорость всего объёма шара.

При ударе цилиндром (рис.5.11,в) количество отлетающих шаров пропорционально длине ударника. В случае цилиндра с размерами d_ц = d_ш и l_ц = d_ш отлетает один шар; при d_ц = d_ш и l_ц = 2d_ш отлетает два шара и сдвигается третий.

Из результатов экспериментов по схеме Э1 следует вывод, что длина ударного импульса (и время соударения) зависит от продольных размеров ударника, а количество воспринятой хронометром (отлетающим телом) механической энергии движения – от скорости ударника. Одновременно можно заключить, что шаровой волновод, как средство эксперимента, объективно отражает процессы, сопутствующие удару.

---

Сконвертировано и опубликовано на http://SamoLit.com/